Some stable LTI systems can be equalized via a direct-inverse method [1]. Here stability means that poles of the system function G(z) are within the unit circle. If G(z) is to be equalized, then the equalizing system H(z) can be constructed by a direct inversion of G(z), i.e., by the following:
where G(z) is the z-transform of the impulse response g(n) of the system to equalize and H(z) is the z-transform h(n) of the equalizing system. The cascade connection of G(z) and H(z) becomes the identity system.
The key requirement for the LTI equalizer H(z) is the system stability. That imposes the additional requirement for G(z). Not only its poles but also its zeroes have to be within the unit circle of the complex plane z as Eq.1 indicates.
LTI systems whose poles and zeroes are located within the unit circle are called minimum-phase LTI systems. Thus, by definition they are stable. They have additional useful property. Their amplitude and phase characteristics are linked to each other by the Hilbert transform. For such systems the amplitude characteristic determines the phase characteristic and vice-versa.
While a wide class of stable LTI systems is composed of minimum-phase systems, only very specific acoustic systems satisfy the minimum-phase assumptions. In general, a linear-phase FIR system is not minimum phase. In the context of reverberation only very special acoustic enclosures and rooms are of minimum-phase (and they are only of minimum phase in an approximate sense).
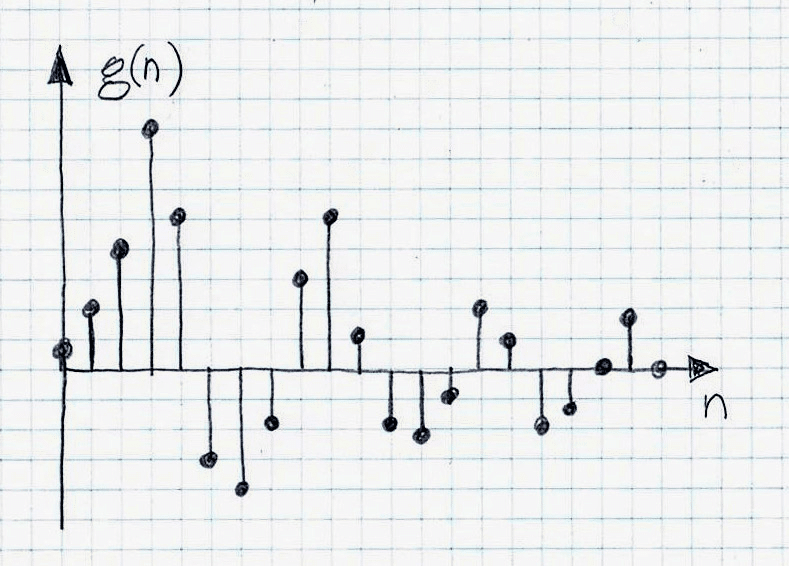
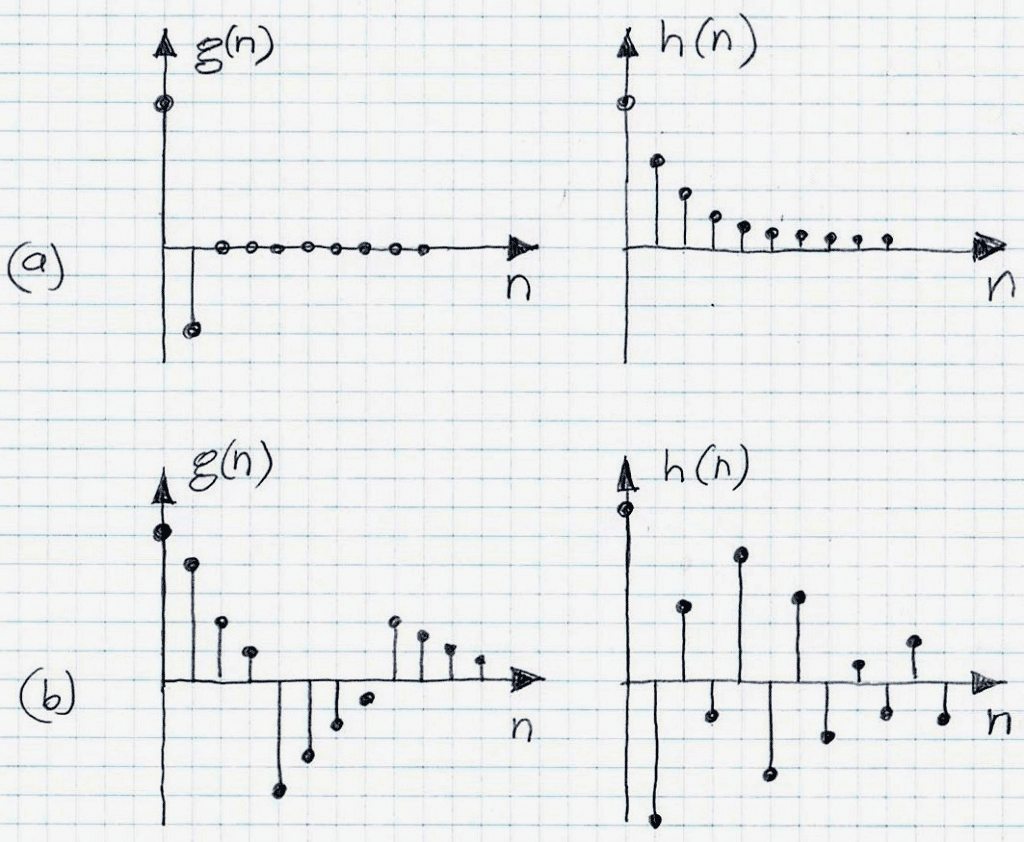
For example, if the impulse response of such systems is composed of early reflections only and if these reflections are such that they are piece-wise decaying (as shown in Figure 1 a and b), then being of minimum phase they can be compensated (equalized that is de-reverberated) by the direct inversion. However, if they do not have that property (example: Figure 2), then the direct inverse become unstable and consequently the direct inversion approach cannot be used for equalization/de-reverberation.
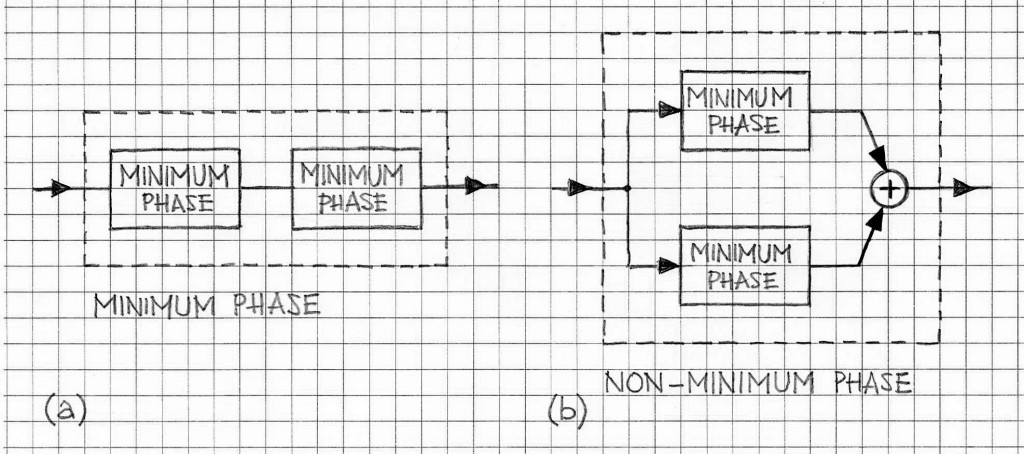
It is also worth noting that if minimum-phase LTI systems are connected in series, the overall system remains minimum phase. The similar property does not hold in the case of systems whose responses are added: the responses of minimum phase system components when added produce a result which is typically not minimum phase (cf. Figure 3).
Non-minimum-phase systems can be equalized /de-reverberated using other advanced methods such as MMSQ/LS method or MINT method (other approaches are mentioned in [1]). Overall, these methods produce good results, however the quality of the results depends on the precision of the approximation used and the computation effort put forward (cf. [2])
VOCAL’s Voice Enhancement solutions include de-reverberation software solutions that have been tested in typical acoustic environments. Custom solutions can be discussed and prototypes can be made provided well-defined specifications are available.
References
- Speech Dereverberation via Channel Inversion and Equalization
- Sequential Separation and De-reverberation” the The Two-Stage Approach, in Microphone Array Signal Processing, Benesty, J, et al., Springer 2008