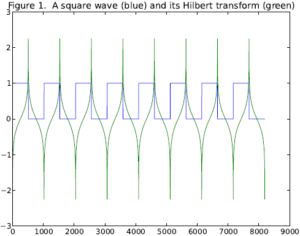
Hilbert Function
The Hilbert transform plays a significant role in signal processing and many other areas of science and engineering such as seismology and medical applications. Examples of applications in signal processing include determination of signal envelopes, regularization of convergence problems in multi-channel acoustic echo cancellation, sampling of bandpass signals for communication, and implementation of modulators.
The Hilbert transform is a linear operator which takes a function u(t) to the same domain. The Hilbert transform is defined by:
with inverse:
where P refers to the Cauchy principal value.
The Hilbert transform is well defined for functions in LP(R) for 1 < p < 1. In addition, it is intimately related to the Fourier transform in that if u(t) is a complex signal, the Hilbert transform phase shifts negative frequency components by π/2 and positive frequency components by −π/2.
The discrete Hilbert transform is related to the discrete Fourier transform in much the same way as for the continuous case. A simple way to compute the discrete Hilbert transform of a time series {ui} is to compute the Fourier transform, zero the negative frequencies, and compute the inverse Fourier transform of the result. However, this method is flawed numerically because the Hilbert transform has a discontinuity at zero frequency, leading to the Gibbs phenomenon. The Gibbs phenomenon causes ripples in the time domain for truncated Fourier series.
To ameliorate this effect, various windowed FIR Hilbert transformers (for example, Bartlett, Hanning, and Kaiser) are used. The properties of Hilbert transformers depend on the coefficients of their impulse response. Essentially, their performance steers a tradeoff between rms ripple amplitude reduction and passband reduction and/or width of transition passband. However, most often, suitable parameter choices yield acceptable results for signal processing applications.
Using these fast FFT based Hilbert transformers, VOCAL can effectively perform operation such as spectral peak determination or modulation domain processing. Contact us today to learn how our extensive knowledge of signal processing applications can help you.
More Information
References
Stephan L. Hahn, Hilbert transforms in signal processing (Artech House, 1996).