Bayesian Inference

Bayesian Inference (BI) is the process of making conclusions from evidence acquired through observations of a given signal, which are formed upon the basis of Bayesian probability principals. BI provides a means to solving practical signal processing applications such as signal prediction, or restoration.

Bayesian inference with regards to parameter estimation aims to provide the best possible approximation of a parameter $\theta$ vector from the information given in an observation y. The best estimate is found by minimizing the risk function, which is proportional to the product of the prior PDF of $\theta$ , the likelihood that the observation signal y occurs given $\theta$ , and the cost of error function, which is often based on the minimum mean square error criteria.

$Risk(\hat{\theta } ) = \int \int Cost(\hat{\theta}\ ,\theta) f_{Y|\theta}(y|\theta) f{_{\theta}}(\theta) dy d\theta$

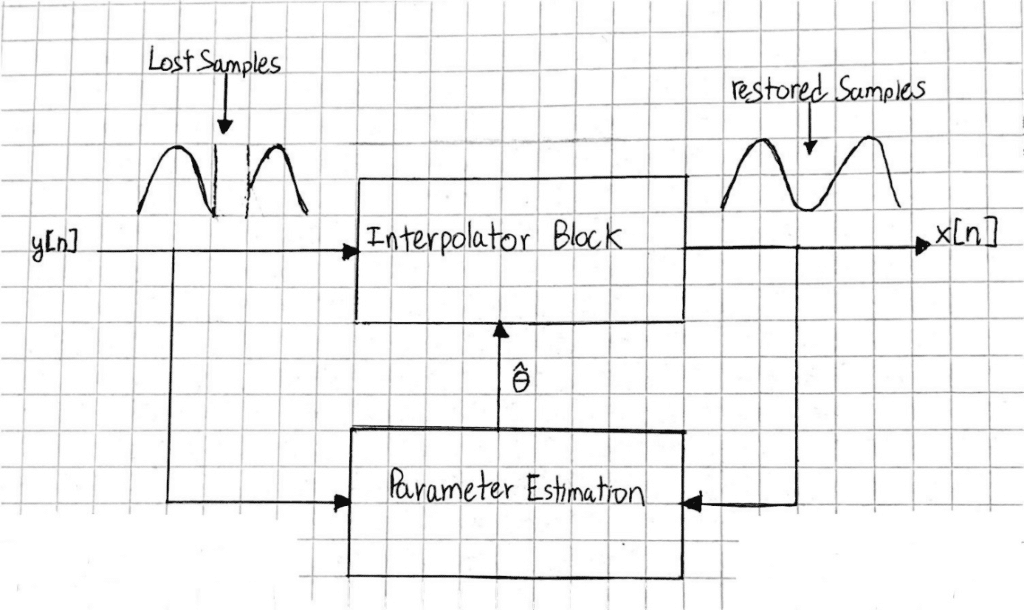
Consider an example where it is desired that interpolation of a segment of lost samples of a signal given N known samples. For this case, it is assumed y is modeled by an autoregressive (AR) process.
y is the observation signal vector: y = X $\Theta$ + e + n
$\Theta$ is the AR parameter vector which is to be estimated
e is random input from the AR model and n is random noise
X is the clean signal vector
The estimate for $\Theta$ can be averaged over the entire observation samples N. As N becomes larger, $\hat{\Theta}$ ̂becomes closer to the actual value of $\Theta$ . A challenge to this problem is that e is purely random, and cannot be estimated in the same way.

Complete Communications Engineering