Often, in the process of analyzing echo cancellation results produced by ECAN (i.e., Line/Network Echo Canceller or Acoustic Echo Canceller), there is a need to establish, with high degree of confidence and via an independent method, what the echo path delay (a.k.a., echo impulse response or echo path delay impulse response) is. Of course, a good approximation of echo path delay is supposed to be available from an ECAN. Some ECAN solutions provide a user interface for downloading echo replica (i.e., a working estimate of the echo path delay).
However, typically, ECAN solutions are not optimized for estimating the echo path delay very accurately. These solutions are optimized for convergence speed and other benchmark parameters and if there is a residual echo (which is a by-product of limited convergence depth) below a predefined threshold, the non-linear processor kicks in and removes traces of residual echo. In this process the echo replica stored in the ECAN memory is not any more accurate. In other words, ECANs are designed to work adequately even with echo replicas of limited estimation precision.
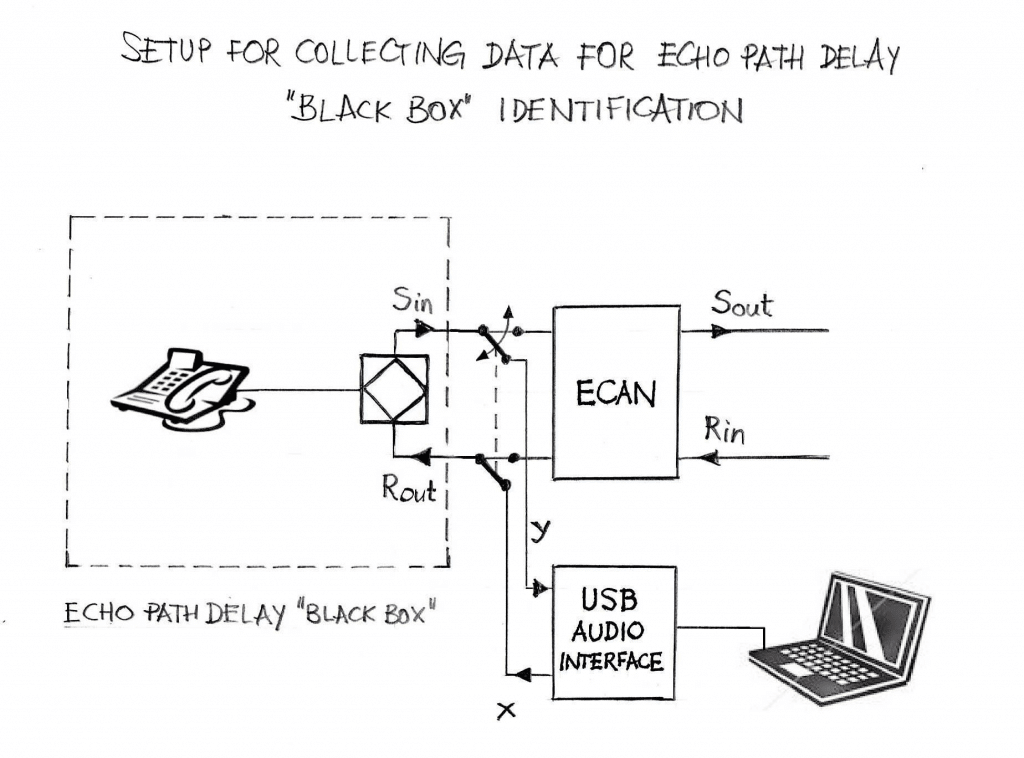
The system setup for collecting data for echo path delay identification off-line is essentially equivalent to ECAN setup, with the following modifications:
- instead of using the far-end signal connected to the Rout port (i.e., the into to the echo path delay “black box”), one shall feed the Rout with white-noise data (we call the input data x);
- instead of using the output from the echo path delay “black box” for the purpose of feeding it to the ECAN and using for the adaptive filter operation to produce adaptively the replica of the echo path delay impulse response, one shall store the output data (we call the output data y).
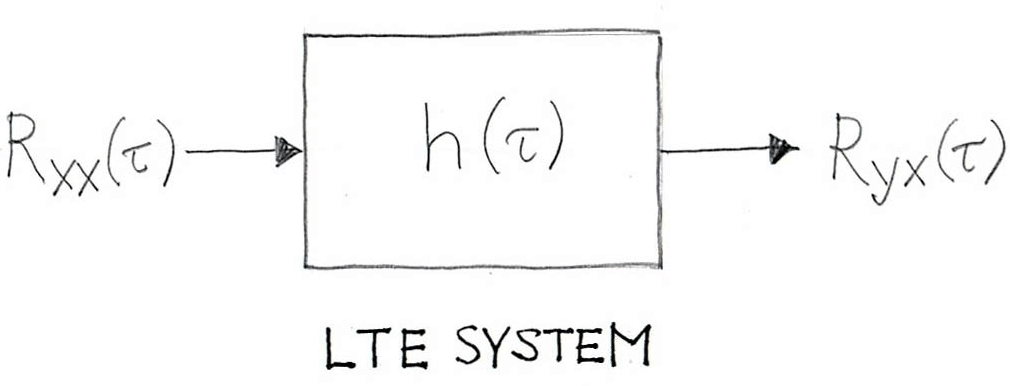
If to the input of a LTE system we supply a random process that is stationary (in strict sense it must be wide-sense stationary and ergodic) then the cross-correlation function between the input and the output is the impulse response. The white noise signals generated by quality random signal generators satisfy, in approximate yet adequate sense, the assumption about the stationarity and ergocity. The theoretical principle behind using white-noise data for identifying the impulse response of the “black box” is illustrated in Figure 2.
Figure 2: If the input signal is a random noise (stationary in wide sense and ergodic), then the cross-correlation between input signal x and output signal y (Ryx(τ)) is a convolution of the impulse response (h(τ)) and the autocorrelation of the input signal (Rxx(τ)). In a specific case, when the autocorrelation of the input signal is Dirac delta (as it is in the case of the white noise) then the the cross-correlation between input signal x and output signal y (Ryx(τ) is the impulse response.
Practical considerations:
- in practice, instead of using a pseudo-random white noise, a band-pass filtered white noise is adequate provided that the band-pass filter pass band is wider than the voice channel bandwidth;
- in order to increase the statistical accuracy of generated results, a sliding window with an overlap is an approach that produces statistically good and practically adequate results.
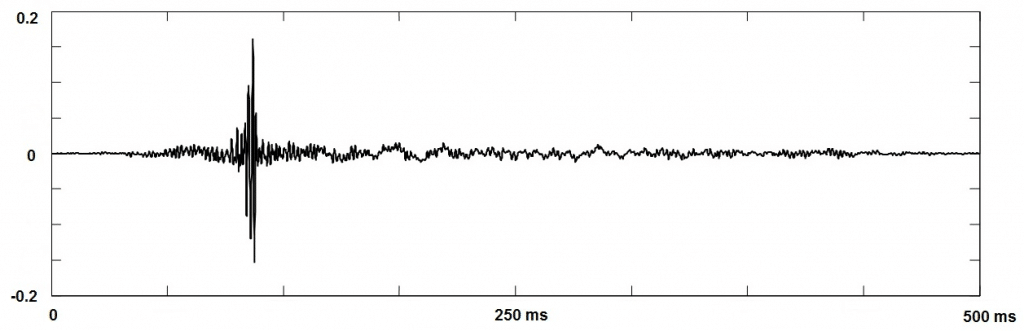
Figure 3 illustrate a real-life example of the echo path delay impulse response generated using the above outlined approach.
More Information