The acoustic feedback problem (a.k.a. Larsen effect) has been a topic of researchers’ and engineers’ attention for over the past five decades. Several groups of solutions have been proposed. Some solutions address the problem by mitigating it. Other solutions attempt to address the root cause of the problem.
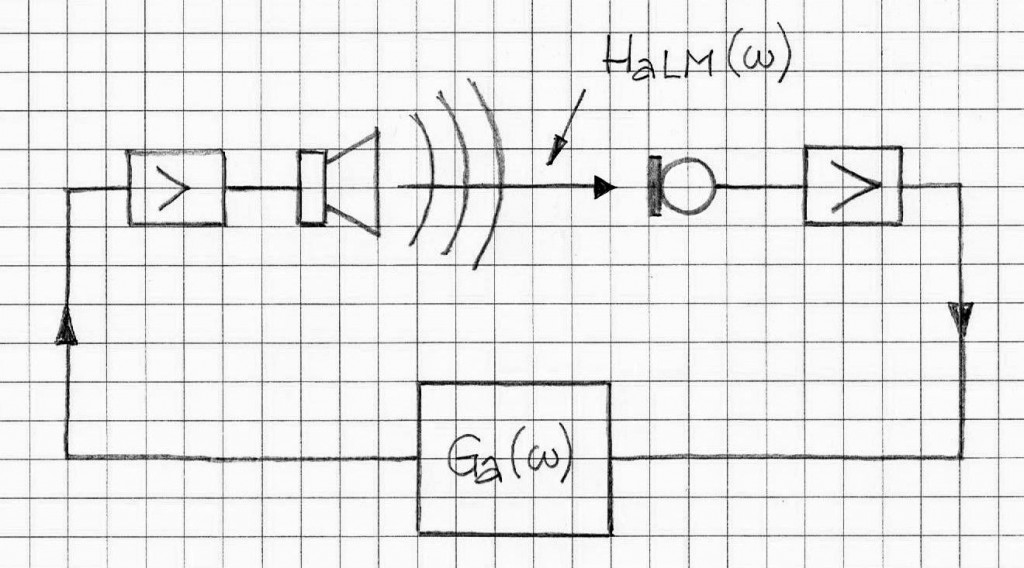
The acoustic feedback problem manifests in many situations where there is a sensor (such as a microphone) and the feedback loop linking the sensor to the sound source, Figure 1. This is a very general system outline and many specific systems and acoustic installations fall into this category of systems.
In generic PA (Public Address) systems it is very common to experience effects of acoustic feedback from the loudspeaker to the microphone. If the microphone is located close to the loudspeaker and the volume knobs are turned up then the conditions for instability may likely occur. Figure 2 depicts the system from Figure 1 in a form of an equivalent system Ta(w).
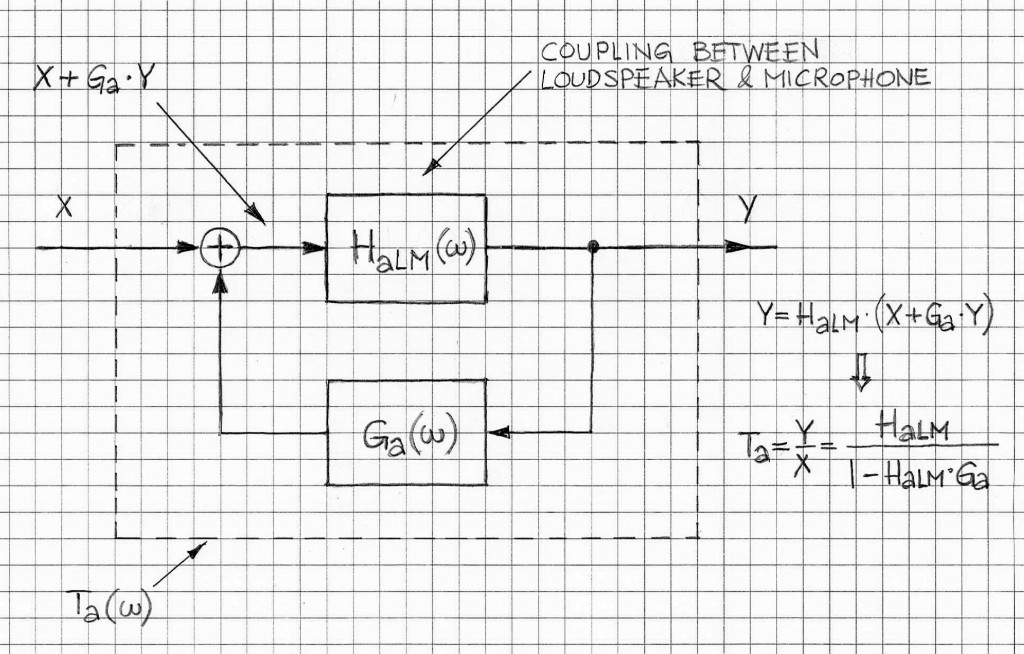
The frequency-domain transfer function of the system in Figure 2 is given below:
Equation 1 is a standard form of the steady-state transfer function in continuous frequency domain. In the case of short-term spectra, Equation 1 is replaced by its short-term version (Equation 2).
The function Da(w,t) expressed as
is referred to as the “loop response” and it is the transfer function of the open loop of the acoustic feedback system. | Da(w,t)| is called loop gain and phase[Da(w,t)] is called loop phase.
Based on the Nyquist stability criterion (cf. Ref. [1]), the closed-loop system becomes unstable if there is a radial frequency w for which
where k is an integer.
There are many other audio/acoustic systems described in a similar fashion as in Figure 1 that are prone to instability. They include Sound Reinforcement Systems, Active Noise Control systems, Hearing Aid Devices to mention a few (Refs. [1, 2]). To control stability of such systems, one needs to make sure that either of the two conditions (as per Equations 4 and 5), or both, are not satisfied. Then the system with the closed loop is stable.
Specifically, the following approaches are used to make sure that conditions for instability, are per Equations 4 and 5, are not satisfied. They are:
- Phase modulation method: this method is using the frequency shifting (FS) approach. For example 5 Hz frequency shift, virtually unnoticeable for an average listener, causes the instability condition to no longer hold. In general, phase modulating feedback control (PFC) that specifically can include sinusoidal phase modulation (PM), frequency modulation (FM), amplitude modulation (AM), and delay modulation (DM), is a reliable way of addressing the acoustical feedback.
- Gain reduction methods – they include:
- automatic gain control (AGC) methods the gain is reduced equally in the entire frequency range by decreasing the broadband gain;
- automatic equalization (AEQ) method, where the gain reduction is applied in selected subbands of the entire frequency range, namely those subbands in which the loop gain is close to unity (cf. Eq. 4);
- notch-filter-based howling suppression method (NHS), where the gain is reduced in narrow frequency bands around critical frequencies, i.e., frequencies at which the loop gain is close to unity.
- Adaptive feedback cancellation method: the method is essentially a version of an acoustic echo canceller-based method (Ref. 2) where the AF is producing the Loudspeaker-Microphone coupling replica and thus the resultant loop response Da(w,t) is no longer close to satisfying conditions as per Equations 4 and 5.
Other approaches to controlling the acoustic feedback include, but are not limited to, signal de-correlation through non-linear distortion insertion and LP encoding. These approaches have some impact (however residual it might be) on signal quality. Minimization of this impact is one of the objectives driving these approaches.
VOCAL’s Voice Enhancement solutions include acoustic feedback control solutions based on acoustic echo cancellation software that have been tested in typical acoustic environments. These solutions can be modified to fit your custom specification and can be used in conjunction with speech-model-based solutions if required. Contact us to discuss your audio application.
REFERENCES
- “Fifty Years of Acoustic Feedback Control: State of the Art and Future Challenges”, by Toon van Waterschoot and Marc Moonen, Proceedings of the IEEE | Vol. 99,No. 2, February 2011
- “Controlling the adaptation of feedback cancellation filters—problem analysis and solution approaches”,, by Henning Puder and Bernd Beimel, Proceedings of the European Signal Processing Conference (EUSIPCO), Vienna, Austria, 2004, p.25-28.