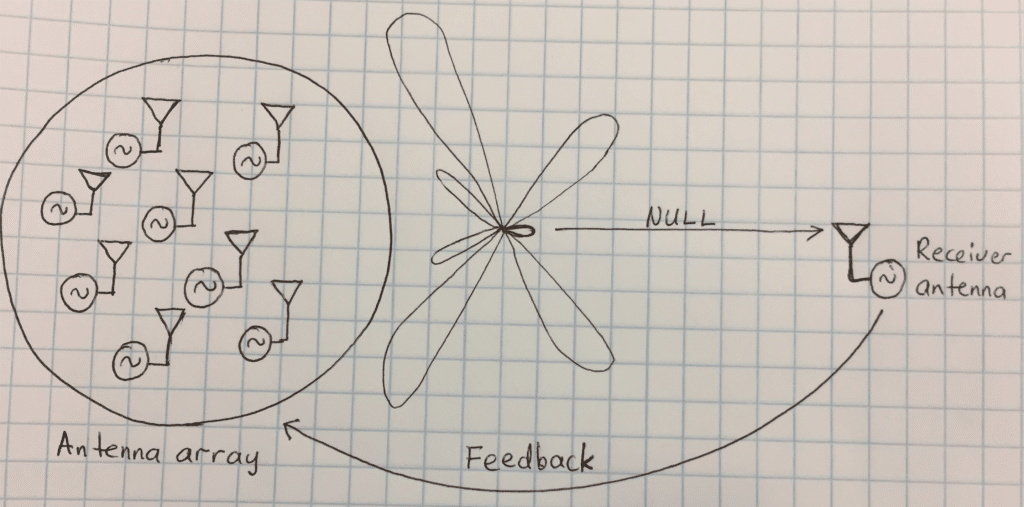
Scalable Distributed Transmit Nullforming

A dual of wireless distributed beamforming is nullforming, a spatial filtering technique used to limit the energy of a beam from a given direction. In distributed nullforming, the problem is as follows: a set of cooperating transmitter nodes transmitting a common signal, spatially align their individual transmit signals in such a manner as to cancel each other out at a designated receiver node. The receiver node cooperates with the transmit array by sending a feedback signal concerning the received signal (RS) strength for the previous epoch. The $k^{th}$ sample at the receiver node follows the following:

$r[k] = \sum\limits_{i=1}^{N} h[i,k]e^{j(\theta_i[k]-\phi_i[k])} +w[k]$

where $h[i,k]$ is the channel gain for the $i^{th}$ sensor at the $k^{th}$ epoch, $\phi_i[k]$ is the channel phase estimation error at the $k^{th}$ epoch, $\theta_i[k]$ is the received phase from sensor $i$ at the $k^{th}$ epoch and $w[k]$ is a zero mean additive noise. The setup is as illustrated in Figure 1.

Figure 1: Distributed transmit nullforming.

Without loss of generality, assume that the channel is stationary, then $h[i,k] = h[i]$ and $\phi_i[k] = \phi_i$ $\forall k$ . To form a null at the receiver node is equivalent to minimizing the cost function:

$J(\theta) = \sum\limits_{i=1}^{N} \sum\limits_{m=1}^{n} h[i]h[m] e^{j((\theta_i-\theta_m) -(\phi_i +\phi_m))}$

The algorithmic solution to minimizing the above cost function is a distributed implementation where each transmit sensor implements the algorithm:

$\theta_i[k+1] = \theta_i[k] -2\mu \hat{h}_i (\cos{(\theta_i[k])}Im\{r[k]\} -\sin{(\theta_i[k])}Re\{r[k]\})$

where $Im\{.\}$ and $Re\{.\}$ denote the imaginary and real parts of the received signal at the receiver node respectively and $\hat{.}$ denotes estimated value. The receiver sends a feedback signal containing the RS for the $k^{th}$ epoch. The scalability of the algorithm is evident since each node independently implements the algorithm by estimating its channel characteristics and using the common feedback signal from the receiver node.

Complete Communications Engineering

Scalable Distributed Transmit Nullforming

More Information