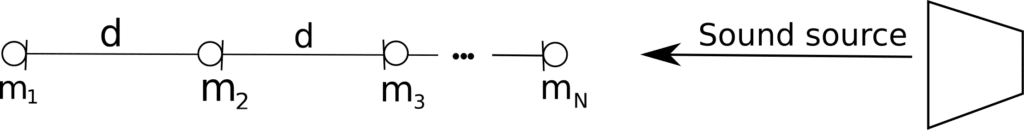VOCAL's Nth Order Endfire Beamformer

An $(N-1)^{th}$ order differential beamforming can be utilized to for an endfire beamformer with arbitrary beamwidth by cascading $\frac{N (N-1)}{2}$ first order differential beamformers together to synthesize a single output.Consider N microphone array as shown in Figure 1:

Figure 1: N microphone array

Instead of performing each first order differential beamformer, it can be shown that each output can be multiplied by a coefficient which follows a binomial expansion pattern. A first order beamformer is obtained by $y(w) = -x_1(w) + x_2(w) e^{-jw\frac{d}{c}}$ , where $y(w)$ is the output and $x_i(w)$ is the input from the microphone $i$ all in frequency domain. It is easy to show that for an $N^{th}$ order beamformer, the output will be:

$y(w) = \sum\limits_{i=0}^{N-1>0} (-1)^{N+i-1} \binom{N}{i} \psi(w)^{i} x_i (w)$
where

$\psi(w) = e^{-jw\frac{d}{c}}$ .

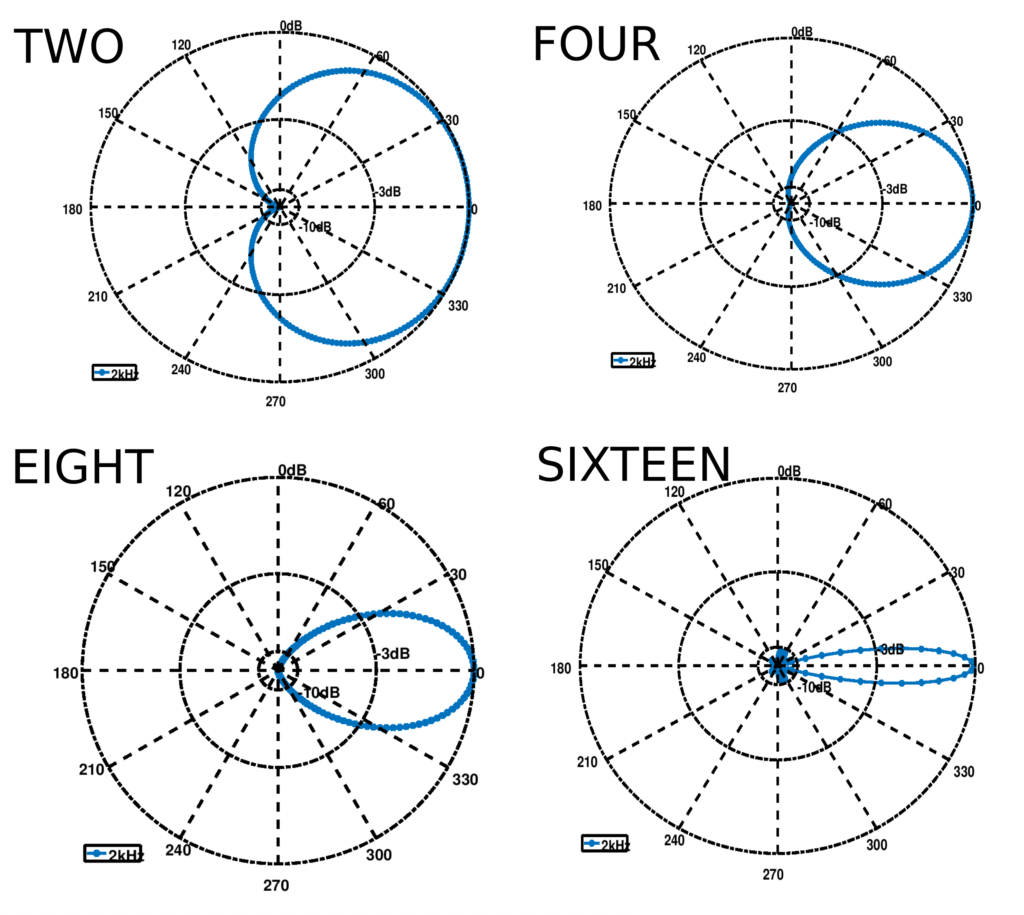
Figure 2 illustrates the differing output beam patterns using different orders but identical settings such as sampling rate and consecutive microphone distance. The effective beam-patterns for a frequency of $2kHz$ is shown in Figure 2 to illustrate spatial noise suppression.

Figure 2: Theoretical spatial filtering beam patterns.

VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

Complete Communications Engineering

Nth order endfire beamformer

More Information