Autonomous detection of gunshots has gained traction as opposed to the reliance on $latex 911$ activated reports due to the non-timely reportage by human actors. The drive for automation is further driven by the unique perspective devoid of multiple conflicting human witnesses. Conventional approaches utilize either acoustic or optical sensors in detecting and ranging the origin of gunshots. In this article, we discuss the use of acoustic microphone arrays to detect the direction of origin/arrival of gunshots.
There are two unique problems that arise from ranging of gunshots. This first is the detection problem. A mechanism has to be in place to discriminate between gunshots and other sound sources if the system is going to be of any use. In this regard, there are three levels of detection that can be employed to tell whether a gunshot related activity has occurred or not. The first step is to check whether the received signal strength, RSI, is above a set threshold $latex T_1$. This threshold can be set to element the triggering of the system on activities such as human speech. The choice of $latex T_1$ is aided by the observation that the RSI of gunshots is at least an order of magnitude to ordinary speech. The first step is essential to limit the amount of computations on any real time operating system that is utilized. The second step is to match the received signal with a template. Here multiple templates can be used to ensure a representation of all gunshot signatures prevalent in the monitored area are captured. A threshold $latex T_2$ can be used to determine whether subsequent to $latex T_1$ a gunshot related activity was indeed captured. The third threshold, $latex T_3$ is required after the received signal passed $latex T_1$ and $latex T_2$. This third threshold is a normalized threshold and Pearson’s correlation coefficient for instance can be used for this tier of checking. If all three thresholds are satisfied, then a gunshot is assumed to have been detected.
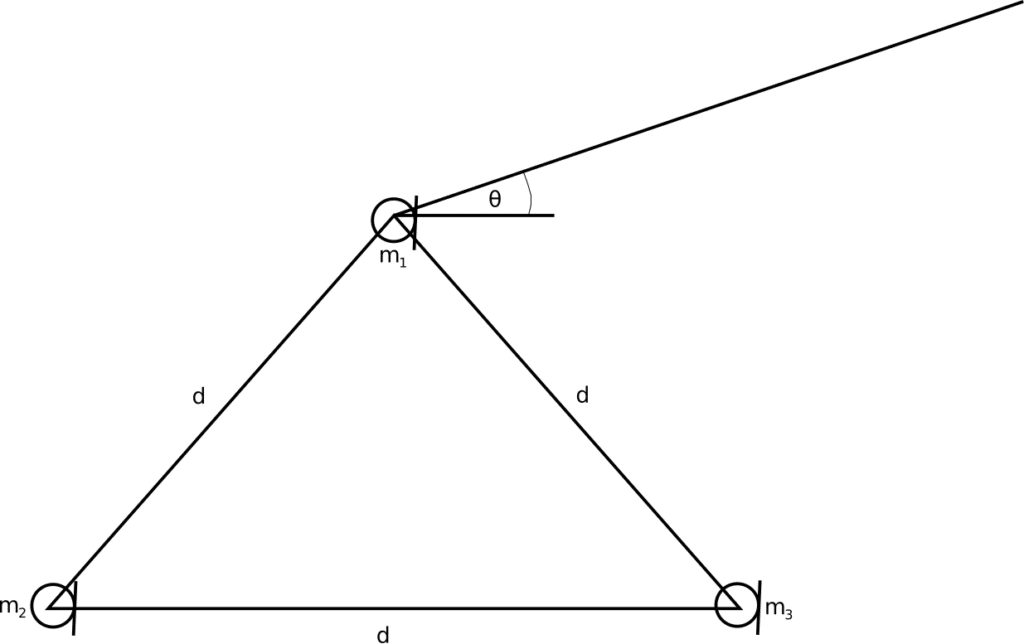
The second problem is the ranging of the gunshot related activity. If the azimuth direction is ignored, then three non co-linear microphones are required to range the gunshot, else three non co-planar microphones are required. In this article we do not consider the azimuth direction. Thus the ranging of the gunshot involves the direction of origin, $latex \theta$ and the distance from the microphone array, $latex r$. Thus the pair $latex (r, \theta)$ completely localizes the origin of the gunshot.
Consider three non co-linear microphones in a topology as shown in Figure 1:
Figure 1: Microphone array for detection of gunshots
Assuming the far field source of gunshot, the angle $latex \theta$ can be found using the equation below.
$latex \theta = \arctan{\left( \frac{\sqrt{3}(\tau_{1,2} -\tau_{1,3})}{\tau_{1,2} +\tau_{1,3}+2 \tau_{2,3}}\right)}$
where $latex \tau_{i,j}$ is the delay between microphones $latex i$ and $latex j$, $latex \{i,j\} \in \{1,2 ,3\}$, and $latex d$ is the pairwise microphone distances apart with the signs of the numerator and denominator determining the quadrant in which the source is located. The delays can be found using any of GCC-PHAT, SRP-PHAT etc. The range $latex r$ can also be found using least squares as shown below:
$latex r = \frac{1}{2} \sum\limits_{i=2}^{3} \frac{d^2 – c^2 \tau_{1,i}^2}{2 c \tau_{1,i} – d (\sqrt{3} \sin{\theta}+(-1)^{i}\cos{\theta})}$
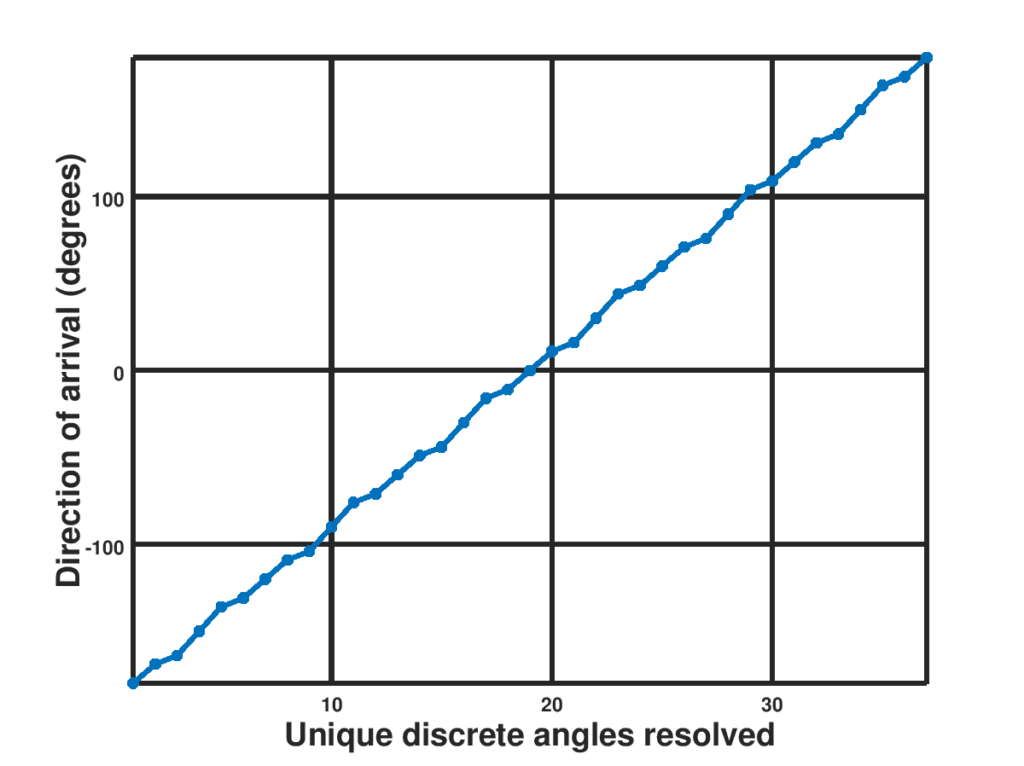
The number of microphones can be increased to reduce the error margins, but in general, three microphones will give a resolution of less than $latex 7\%$ absolute error in the direction of arrival estimates,which will be propagated in the denominator. The resolution of $latex \theta$ is as shown in Figure 2 below.
Figure 2: Three microphone array topology
VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!