Full circle DoA estimation for RTOS using least squares

Speech processing on real time operating systems (RTOS) more often than not require estimates of the direction of arrival (DOA). Due the the time and computation constraints on RTOS platforms, most sophisticated algorithms are impractical. Thus, instead of MUSIC like algorithms for estimating the DOAs, time difference of arrival algorithms are leveraged to give reasonable estimates for most applications. The topology of the microphone array has to also be taken into consideration. A linear array is unable to distinguish signals from the front or the back due to spatial ambiguity. Thus a minimum of three non co-linear microphones are required to have a full view in two dimensions. In a three dimensional plane, a minimum of four non co-planar microphones will be required. In most applications a two dimensional resolution of the DOA suffices.

Consider a far field speech impinging $n+m$ microphones and suppose it is desired to estimate the DOA. This is depicted in Figure 1 below:

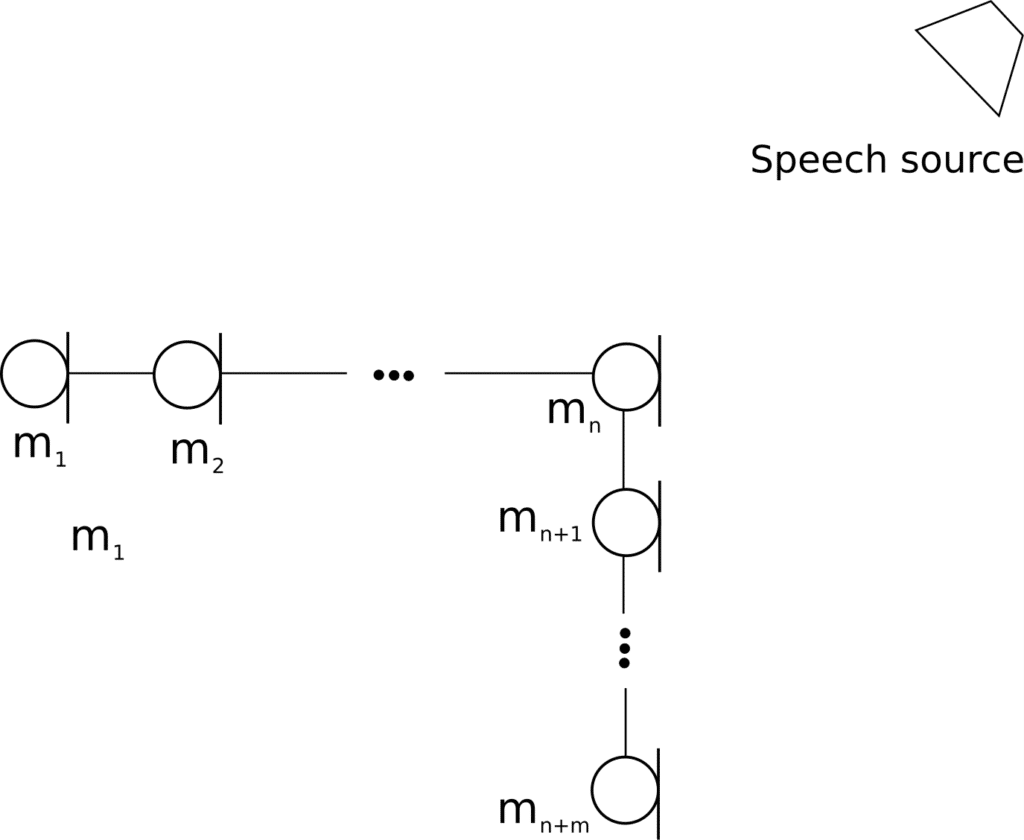
Figure 1: $n + m$ non co-linear microphone array

The signal at each microphone obeys:

$x_i(t) = s(t - \tau_i) + \nu(t)$

where $\tau_i$ is the delay from the source. Its is easy to verify that the time difference of arrivals (TDOA) of the horizontal array will obey:

$\tau_j - \tau_i = \tau_{i,j} = (j - i) \frac{d}{c} \sin{\theta}$

while the vertical array will obey:

$\tau_j - \tau_i = \tau_{i,j} = (j - i) \frac{d}{c} \cos{\theta}$

where $d$ is as shown on Figure 1 and $\theta$ is the DOA with respect to the ordinate. We could also use the TDOA between horizontal array and vertical array depending on the computational resources available. For $n+m$ microphones, we get $\frac{(n+m)(n+m-1)}{2}$ unique tuples from which the TDOA can be estimated. Using only the vertical and horizontal arrays will result in a reduction to $\frac{(n)(n-1)}{2} + \frac{(m+1)(m)}{2}$ unique tuples. This will lead to a system of equations given as:

$\underbrace{\begin{bmatrix}\tau_{1,2}\\\tau_{1,3}\\\vdots\\\tau_{1,n}\\\tau_{2,3}\\\vdots\\\tau_{n-1,n}\\\tau_{n,n+1}\\\tau_{n,n+2}\\\vdots\\\tau_{n,n+m}\\\tau_{n+1,n+2}\\\vdots\\\tau_{n+m-1,n+m}\end{bmatrix}}_{Y}=\underbrace{\frac{d}{c}\begin{bmatrix}1&0\\2&0\\\vdots&\vdots\\n-1&0\\1&0\\\vdots\\1&0\\0 &1\\0&2\\\vdots&\vdots\\0& m\\0&1\\\vdots&\vdots\\0&1\end{bmatrix}}_{A}\begin{bmatrix}\sin{\theta}\\\cos{\theta}\end{bmatrix}$

Then the least squares solution becomes

$\begin{bmatrix} \sin{\theta} \\\cos{\theta}\end{bmatrix} = (A^T A)^{-1} A^T Y$

It should be noted that $(A^T A)^{-1} A^T$ can be computed once and then only $\frac{(n)(n-1)}{2} + \frac{(m+1)(m)}{2}$ additions and multiplications are required to estimated $\sin{\theta}$ and $\cos{\theta}$ respectively.

The choice of sampling Frequency and/or $d$ , together with the number of microphones can be used to determine the resolution of the returned DOA. It should be noted that we could use a square topology but that will not provide extra information but only reinforce the given estimates by removing noise from the estimates. In the noise free case, the extra half topology from the square configuration provides no extra information for estimation.

VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

Complete Communications Engineering

Full Circle Direction of Arrival Estimation RTOS Using Least Squares