Video compression is an essential part of video processing devices. Many video compression algorithms utilize a block transform approach. One of the consequence of this approach is the presence of blocking artifacts in the decoded video.
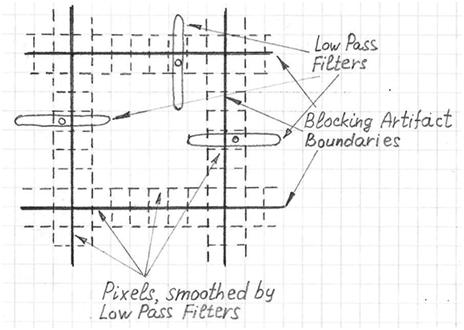
The visibility of the artifacts is associated with the compression ratio that defines the bitrate of the compressed bitstream. Blocking artifacts may be visible in flat areas (areas where for DCT transform DC value is high and AC values are low), texture areas (especially for low bitrate), and edge areas. The artifact appears as a distinguishable set of squares interleaved with the image.
The best time to reduce blocking artifacts is immediately after the block decoder since the location of block boundaries is known. The artifact can be reduced by horizontal low pass filtering of two pixels surrounding the vertical boundary of the block, and vertical low pass filtering of two pixels, surrounding the horizontal boundary of the block.
The blocking artifact reduction block may not be located after the block decoder, in which case there is no direct information about the boundaries of the artifact. In this case a blocking boundaries detector has to be associated with the blocking artifact filter. The blocking boundary detector has to identify the location of boundaries of periodic square structures within the image. It will only identify a boundary if the difference between adjacent pixel levels is small (below some particular threshold).
There is a method to reduce blocking artifacts in flat areas using a small transition spatial filter. In some area surrounding the current pixel with value x, a spatial 2-D low pass filter (for example having aperture 3×3 pixels) is applied. The result of the filtering is F. The output value of the small transition filter is:
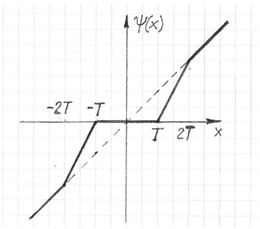
y = F + Ψ(x–F),
where Ψ() is a nonlinear function shown on Fig.2 and defined by the threshold T. This threshold specifies the level of the transition for which the spatial filtering is applied. If the transition is greater than the threshold, no filtering happens.