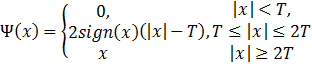Noise Reduction using Spatial Level Control Filter is used in video processing to reduce noise. In many cases noise reduction also increases the perceptual image quality.
A high level of spatial filtering may cause smoothing or removing of small details, softening or blurring the image. To resolve this issue, spatial filtering is only applied for small transitions defined by a threshold T.
There are many spatial filters: 2-D block, 2-D cross, vertical, horizontal, diagonal or any other special shape. Fig.1 shows an example of a 2-D filter aperture where the current pixel is denoted as “e”.

For 2-D 3×3 low-pass block filter the filter coefficients are: be = ¼; bb = bd = bf = bh = 1/8; ba = bc = bg = bi = 1/16.
For 2-D 3×3 low-cross filter the filter coefficients are: be = 1/2; bb = bd = bf = bh = 1/8; ba = bc = bg = bi = 0.
For a horizontal filter: be = 1/2; bb = bh = ¼. All others are zero.
For a vertical filter: be = 1/2; bb = bh = ¼. All others are zero.
For one diagonal filter: be = 1/2; ba = bi = ¼. All others are zero.
For another diagonal filter: be = 1/2; bg = bc = ¼. All others are zero.
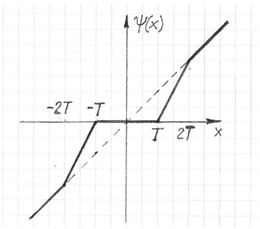
The filtered value, Fe, is subtracted from the current value xe. The difference (xe – Fe) goes through the nonlinear function Ψ() and is added back to Fe. The output of the noise reduction block is ye = F + Ψ(x–F), where the nonlinear function Ψ() is:
From the filters listed above, any subset may be applied in sequential order. For each filter, the optimal threshold has to be individually identified.
The spatial filter described above is able to reduce many kinds of noises such as Gaussian noise, flat area blocking artifact or small mosquito noise.