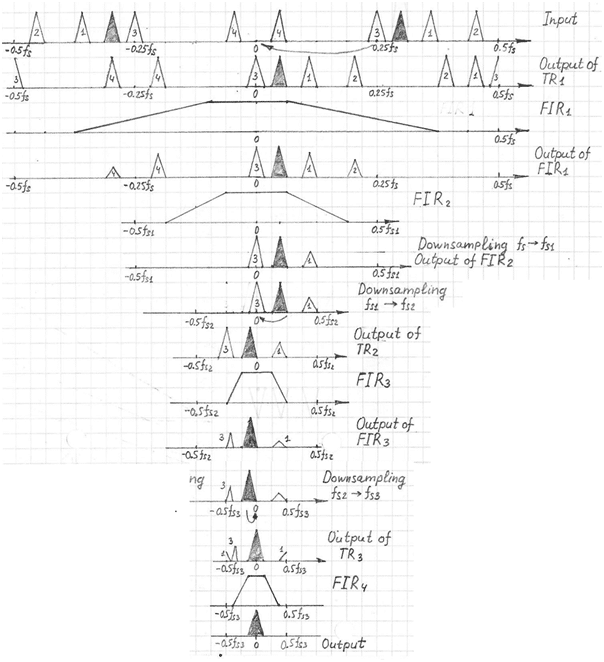
In signal processing. filtering to extract only a narrow part of the input spectrum is a common problem. For example, the input may consist of multiple adjacent video or audio channels and only one has to be filtered out.
An efficient way to do this is using a cascade of simple FIR baseband filters, downsamplers and trivial rotators. Almost all FIR filters in the system are antialiasing FIRs for downsampling.

A trivial rotator is a rotator that shifts the frequency by Δf = fS/2n, where fS is the sampling frequency and n is an integer number. The frequency shift can be done by multiplying the input signal by e-j2πΔft. A negative exponent will downshift the frequency. The simplest rotator is when n=2. In this case e-j2πΔft is the following sequence of samples:
1; j; -1; -j; 1; j; -1; -j.
In this case, the rotator does not require multiplications; only sign changes and demultiplexing.
For n=4, the sequence of samples is:
1; 0.7071+0.7071j; j; -0.7071+0.7071j; -1; -0.7071-0.7071j; -j; 0.7071-0.7071j.
In this case, only multiplication by the coefficient 0.7071 is required.
Figure 1 shows an example of narrowband signal extraction by a sequence of trivial rotation, filtering by antialiasing FIRs and downsampling. While Figure 2 illustrates an example of the output of narrowband signal extraction in the frequency domain.