An Embedded Zerotree in wavelet image compression enables video decoders to efficiently zero out all related higher-scale coefficients. Every wavelet coefficient at a given scale can be related to a set of corresponding coefficients at the next finer scale. If a particular coefficient is zero, and all corresponding coefficients in consecutive layers are also zero, this coefficient is tagged as the root for a zero tree and the rest of zero coefficients are not encoded. The sequence of trees are encoded by entropy coders.
Wavelet compression is a very efficient technique for image/video compression. It is based on the wavelet transform that provides a multi-scale representation of images and video in the space-frequency domain. The inherent scalability property allows wavelet encoded video to be simultaneously dedicated for devices with different resolutions. Wavelet based compression does not have noticeable blocking artifacts, like those found in transform based compressions.
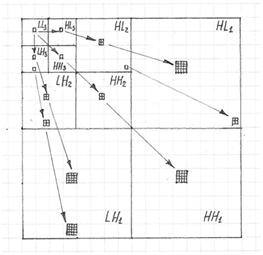
The wavelet transform is based on N layers of consecutive repetition of similar 2-D wavelet decompositions. As illustrated in Figure 1, the first layer takes the original image with resolution WxH and applies horizontal and vertical low-pass (scaling) and high pass (wavelet) filtering followed by downsampling by 2.
The result of wavelet decompositions is four 2-D bands of the original image, each with resolution W/2 x H/2. These bands are called LL1 (low horizontal, low vertical), HL1 (high horizontal low vertical), LH1 (low horizontal high vertical) and HH1 (high horizontal high vertical) bands.
At the second layer, the same decomposition is applied but only for the LL-band of the first layer. The result is four bands LL2, HL2, LH2 and HH2, each with resolution W/4 x H/4. The next layer processes LL2, and so on. After N layers of wavelet decomposition the result is represented as a set of bands HLn, LHn and HHn, n = 1,..N, and LLN.
At the reconstruction side there in an opposite process using reconstruction scaling and wavelet filter followed by upsampling. From decomposed bands (for no quantization case) it is possible to reconstruct the source image exactly.
Wavelets are particularly good at localizing edges and texture. Since natural images in general have a low pass spectrum the HLn, LHn and HHn have a lot of small close to zero coefficients. The wavelet coefficients will, on average, be smaller in the higher frequency subbands than in the lower frequency subbands.
After applying quantization, there are a lot of zero coefficients. Specifying a zerotree allows the decoder to “track down” and zero out all the related higher-scale coefficients.