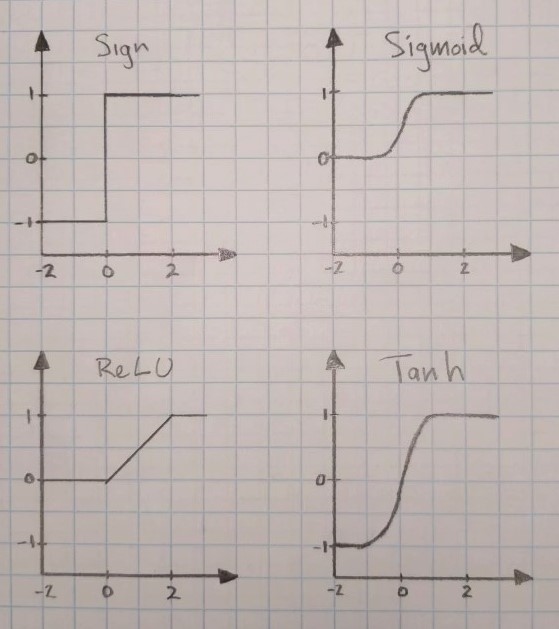
The advantage of neural networks is their ability model non-linear systems. Neural Networks without activation functions (or with identity activation functions) are linear regression models, and adding more layers does not help with classification. The enhanced ability to model unknown systems come from activation functions, which are required for mapping non-linearly separable classification problems into a linear separable space. The commonly employed activation functions are shown in the image below:
The sign function is only applicable to binary classification problems, such as a voice activity detector, and cannot be used for non-binary classification. The sigmoid functions are used when the output node is meant to represent the probability of the observation and are good for creating loss functions derived from the maximum-likelihood models. The Rectified Linear Unit (ReLU) function, as discussed in the Vanishing Gradient, has both linear and nonlinear properties meant to help solve the vanishing gradient problem. The hyperbolic tangent function (tanh) is related to the sigmoid function in that the output is rescaled to -1 to 1. This activation function is preferred when output nodes should have positive and negative values, which is desired in the hidden layers. Not shown is the hard Tanh function, which is the ReLU equivalent to the tanh function. Knowing where you are in the network and what the desired range of output should be helps with the selection process.