Noise Reduction via Hidden Markov Model (HMM)

A Hidden Markov Model (HMM) is a powerful statistical tool with many practical applications in temporal pattern recognition. These applications include speech enhancement, de-noising of speech, speech recognition and related tasks. At present there is limited number of efficient approaches to de-noising of speech based on single channel operations (i.e., where there is only one sensor/microphone available in the system under consideration).  HMM-based approach provides a viable alternative to other methods such as spectral subtraction, and, in many ways, is considered as more powerful, generally speaking. The main reason for being more powerful is that unlike the spectral subtraction approach, which is based on the assumption that the distractor (i.e., undesired signal such as  noise) is stationary, the HMM is not bounded by this limiting assumption: it is intended to work with non-stationary distractors as well.

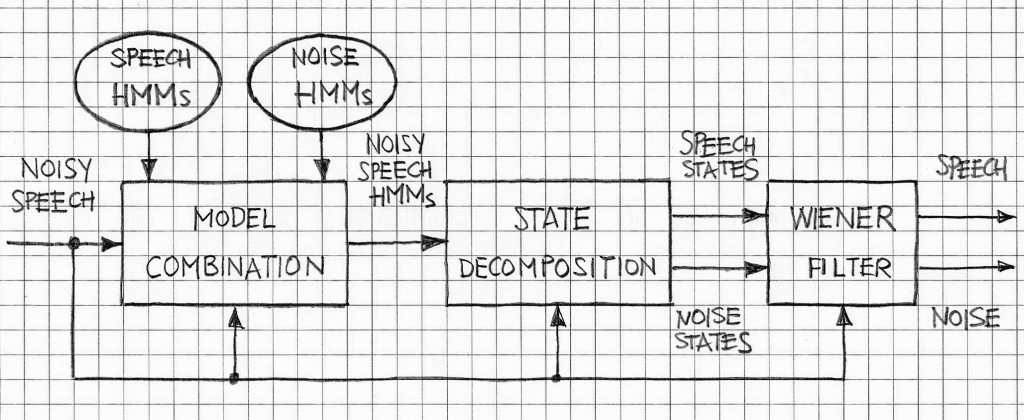
The high-level view of the noisy speech enhancement based on the HMM approach is shown in Figure 1. The system performs the following functions:

1. Based on the pre-determined HMMs for noise and separately pre-determined HMMs for speech, the Model Combination block forms the noisy speech HMMs;
2. Based on the current noisy speech at the input, the Model Combination block estimates and selects the best combined noisy speech HMMs, in a form of input data to the State Decomposition block;
3. State Decomposition produces speech states and noise states as output data, for the given noisy speech states;
4. Given the speech states and noise states inputs to the Wiener filter block, it produces estimations of speech and noise.

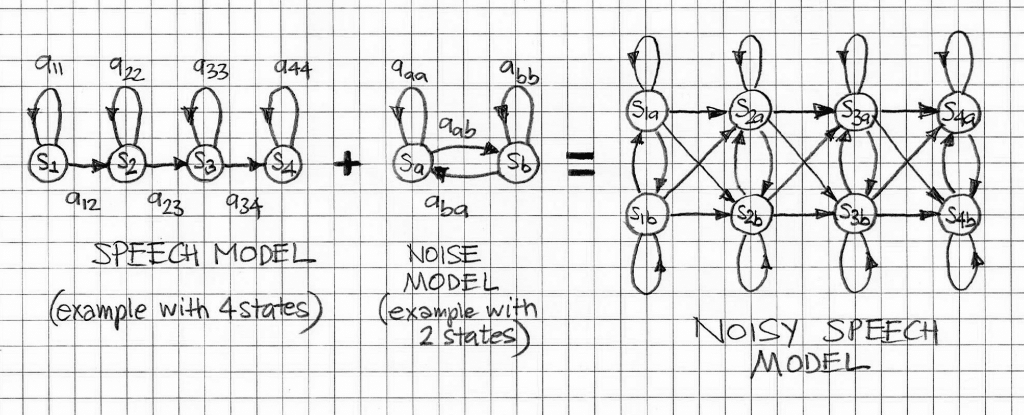
Regarding function/step 1 – Model Combination – it also requires that the current SNR value be estimated for use in the approximations of mean vector and the covariance matrix of the noisy speech by adding the mean vectors and the covariance matrices of the speech models and noise models. As an example, Figure 2 illustrates the combination of a 4-state HMM of a speech signal with a 2-state HMM of noise (note that in practice the numbers of states for speech and noise are much greater).  Since speech and noise are assumed as independent processes (and this assumption is valid in most practical applications), each speech state must be combined with each noise state to produce the noise speech model.

Regarding function/step 2 – State Decomposition – it can be by performing the following:

• Estimation of the maximum likelihood (ML) of combined noisy HMM for the noisy signal;
• Generation of the ML state sequence from the ML combined model;
• Extraction of the signal states and noise states from the ML state sequence of the ML combined noisy signal model.

Regarding function/step 3 – HMM-Based Wiener Filters – it can be implemented as follows:

• Combine the signal and noise HMMs to form the noisy signal HMM;
• Generate the ML combined signal model;
• Generate the ML state sequence of speech and noise;
• Apply the ML estimates for the power spectra of the signal and the noise as inputs to the Wiener filter sequence;
• Use the state-dependent Wiener filter sequence to produce signal separation, i.e., to produce the speech and noise estimates.

The HMM approach to Speech Enhancement  falls into the category of generic speech-model-based approach; more information related to this approach to Speech Enhancement solutions is available in [2].

VOCAL’s Voice Enhancement solutions include noise reduction software solutions that have been tested in typical acoustic environment. These solutions can be modified to fit custom specifications and they can be used in conjunction with speech-model-based solutions if required. Contact us to discuss your speech application.

REFERENCES

1. Hidden Markov Models (Section 5), Advanced Digital Signal Processing and Noise Reduction,  by Vaseghi, S V., A John Wiley and Sons, Ltd. 2001
2. Model-Based Speech Enhancement
3. Voice Enhancement Design