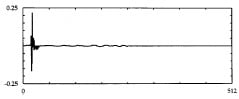
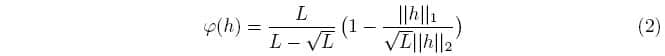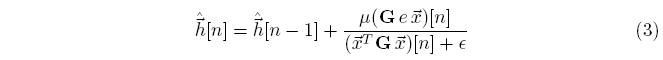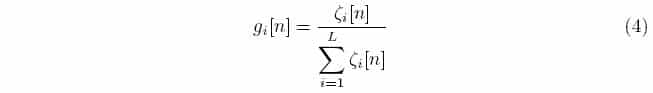In a typical sparse echo path, the meaningful information is packed in the early part of the response. From a computational resources point of view, after the early burst, we would reach a point of greatly diminishing returns. From a convergence point of view, trying to model the rest of the impulse response may end up doing more harm than good. The finite word-length effect will create quantization noise comparable to the LSB of the late response, which will not only result in a misadjustment floor but also may lead to instability in the adaptive attempts to correct it.
Figure 1: Example of a Sparse Echo Path [1]
We are therefore well motivated to develop a means by which to capture only the most essential information while leaving the largely irrelevant and potentially dangerous information for the echo suppressor block of our acoustic echo cancellation (AEC) system. There are many ways to do this, but the first true solution to this problem came from [1]. It was there that Donald Duttweiler developed the Proportionate Normalized Least Mean Square Algorithm for echo cancellation.
Sparsity Measure
Sparsity is a measure of the portion of the echo path that is zero or at least trivial compared to the portion that is not. With respect to the sampling time, sparse echo channels can often be modeled as a linear combination of unit impulses:
Where Ф is the support of the room impulse response function. In practice, it may be difficult to precisely determine its cardinality due to many elements being not exactly zero. To get around this problem, we define a measure φ on the set Ф based on Euclidean norms. One common example is φ: Ф → R[0;1] based on the l1 and l2 norms:
Where L is the length of the entire impulse response and ||∙|| denotes the norm. As the room impulse response is often normalized, this function is a simple linear interpolator.
The Proportionate NLMS Algorithm
The basic idea behind the PNMLS echo cancellation algorithm is to assign the coefficients that capture most of the energy in the room impulse response the largest adaptation step-size. In doing so, we are effectively assigning more importance to these coefficients, and thus this echo path estimate will converge much quicker. This algorithm’s structure is the same as the NLMS, except that the coefficient update equation is defined as:
Where G[n] = diag[g0, …, gL–1][n] is a diagonal matrix and gi[n] is the ith coefficient adaptation step-size given by:
Where ζi is the ith proportionality function defined as:
Where f is the activation factor defined as:
Where θ is chosen to prevent the algorithm from being stuck at zero, and ρ is a chosen to ensure individual coefficients that are smaller than the maximum magnitude are actually updated. As with most regularization parameters, they are chosen experimentally, so please see [1] for the discussion.
Since its inception, there have been many versions of this algorithm. For further study, please see the literature on sparse echo cancellation algorithms such as the Improved PNLMS, Signed Regressor PNLMS, and the Individual Activation Factor PNLMS among others. All of these algorithms attempt to incrementally solve the problems of the proposed PNLMS algorithms that came before.
Processing Structures
As alluded to before, there are many ways to define g→[n] or even Ф. In this section we will give some alternative methods for both. Besides redefining the sparseness measure φ, there are means to directly estimate ![]() ̅ by attempting to find the φ ∈ Ф directly.
̅ by attempting to find the φ ∈ Ф directly.
For instance, one method is to use a sliding window. By comparing the power found in the window as it moves along, you can find the neighborhood of Ф as the set that contains the most energy. Alternatively, you can find the center of the interval by comparing the smoothed cross-correlation of the far-end and near-end signals while in a single-talk state.
Regardless of which method you use, you still need to find the boundary of Ф. One way to do this is to simply place a fixed number of taps at the beginning of the sparse echo path. This approach is valid because the room impulse response is typically monotonically decreasing. Alternatively, you can use different fixed tap lengths for a variety of filters, and pick the one that gives you the best results.
Another way to do this is to look for a pre-defined number of maxima. Once this set is found, place the center of the interval at the global maximum. Then, the distance to the Nth local maxima in both directions illustrates the boundary. Else, you can simply find the global maxima with a large window, and reduce the size until the change becomes drastic, either in terms of power or correlation.
Alternatively, you might split the set, and distribute your taps according to some function across the N reflections having the required amount of your statistic, wherever they may lie. Alternatively, you might want to use your system’s voice-activity-detector to do this job. By detecting where the speech is located in the far-end signal, your VAD can automatically decide the set of taps to use.
Another method is to look for the sensitivity in the output with respect to the change in the tap coefficients. The most sensitive coefficients are given the smallest step size, while the least are given the largest adaptation rate. The sensitivity can be found by changing the adaptation step-size by a constant and observing the results.
As alluded to before, the actual adaptation gain can be determined by the power of the tap itself, by its correlation, by its absolute value, or by its sensitivity. Such statistics can be calculated using a shadow filter, by using a training signal, or by using recursive measures in the foreground. The exact measure, way to find it, and structure of the system is up to the individual designer.
References
[1] D. Duttweiler, “Proportionate Normalized Least-Mean-Squares Adaptation in Echo Cancelers” IEEE Transactions on Speech and Audio Processing, vol. 8, no. 5, September 2000, pp.508-517