Speech enhancement devices, when available in the form of reference design or an early prototype, are typically evaluated in an environment that does not necessarily reflect real-life conditions. When the prototype matures, evaluations are done in conditions closer to real-life. A typical office or a conference room environment becomes one of the ad hoc choices for the testing environment.
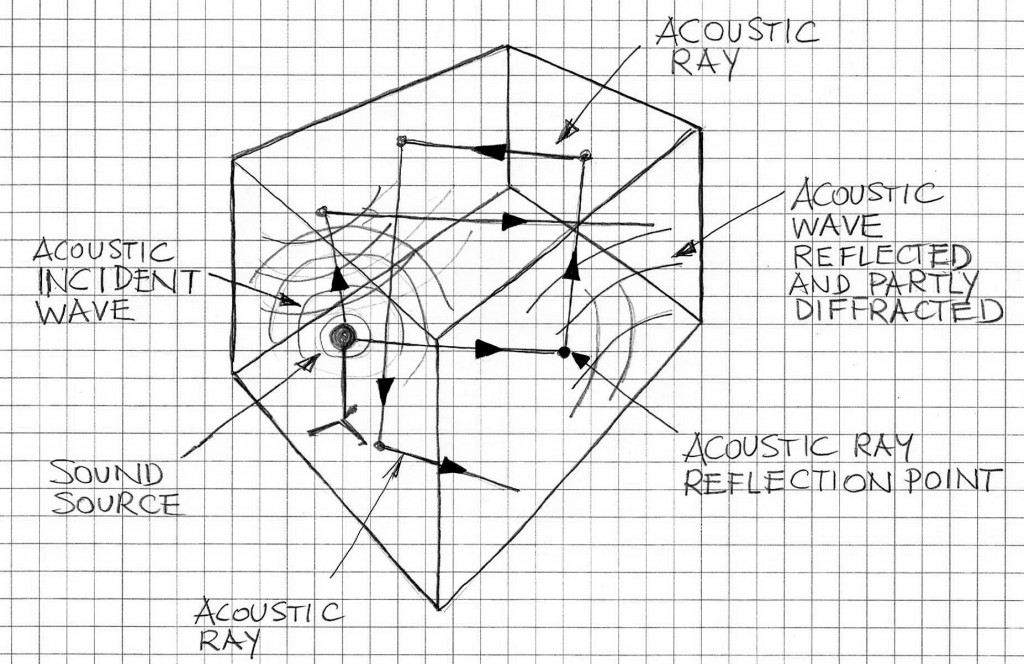
A room, as an example of acoustical environment, manifests effects associated with early and late reflections of sound. For that purpose, it is required that sound propagation models in reflective spaces be considered and analyzed.
Figure 1 illustrates the concept of ray tracing versus wave propagation modeling for applications related to evaluating and modeling acoustic properties of rooms and other closed spaces. Results of modeling acoustic properties of rooms allow for estimations of room reverberation effects, including tangible measures of this effect such as RT60 (cf. [2]).
In this context some selected models of room reverberation are briefly discussed in the following paragraphs. The main source of reference for this discussion is [1].
Intuitive Model of room reverberation is an unstructured and ad hoc observation-based list of effects following an excitation of the room by an acoustic pulse (for example, a hand clap). When the room’s acoustic environment is excited by such simple excitation, the experimenter, or listener, notices that the sound energy decays with time. Apart from audibly distinct sound reflections from walls and other objects, followed by sustaining and decaying sound effect when distinctive reflections are no longer noticeable. These ad hoc observations lead to the intuitive model of room reverberation. Typically such a model does not use any calculus or other technical means to closer describe the room acoustic characteristics. Such a model is tainted with experimenter’s bias (a.k.a., research bias) and thus is in many ways incomplete and not adequately accurate.
Finite Element Models are based on numerical methods of solving partial differential equations governing the sound propagation with boundary conditions reflecting geometric positions of room walls and other objects in the acoustic filed as well as reflecting the acoustical properties of these objects such as absorption coefficients and many others. The Finite Element Models are taking advantage of powerful numerical methods such as Finite Element Method (FEM) and Boundary Element Method (BEM) and they reflect quite adequately the real behaviors of acoustic environment when excited by acoustic sources.
Within the class of Finite Element Models of rooms there are other related approaches such as the ones based on the Finite-Difference Time-Domain (FDTD) method, which, according to published reports, are better suited to reflect audible behavior of the numerically simulated phenomena (cf. [1]).
Other approaches to modeling room reverberation effects include (but certainly not limited to) the following:
Digital Waveguide Mesh (DWM) technique that numerically models room acoustics and includes wave propagation effects such as diffusion, scattering, diffraction and other wave effects (including non-linear effects if the sound excitation level warrants such an approach);
Ray Tracing (RT) technique, which is based on significant simplifications of sound propagation and, by definition, does not directly include wave effects; that approach is very common for analyzing acoustics of large rooms and halls for which the ratio of the largest acoustic wave in the frequency spectrum under consideration and the minimum geometric distance or linear size is smaller than the factor of 1/10 (which is a customary and simplified benchmark for applicability of the ray tracing technique); in fact this techique predicts correctly the acoustics of a room in the frequency band where the largest wavelength is small in comparison with the linear dimensions of objects in the room or the room dimensions. For example, in the case of a medium size office with a desk, the wavelength λ must satisfy the following condition λ << 1 m and that condition translates into the smallest frequency (i.e. fmin >> 344 Hz) for which the technique produces meaningful results. So practically, the frequency band for use in this case starts approximately with 3kHz, which is a very significant limiting factor.
VOCAL Technologies practices include characterization of acoustical environment within which the voice enhancement devices are verified and evaluated. These practices include estimations of RT60 full band and in sub-bands (such as in octave bands) as well as and of critical distance parameter (Dc). In some cases numerical simulations of room characteristics are also included. Contact us to discuss your speech application testing requirements.
REFERENCES
- Speech Dereverberation (Signal and Communication Technology series), Patrick A. Naylor and Nikolay D. Gaubitch (editors), Springer-Verlag London Limited 2010
- ON RT60 ESTIMATION
- Echo Cancellation Design