Correlation Techniques

In audio or speech signal processing, we often encounter signal lineup problems. They can happen in either time or frequency domains. This short article describes such techniques in both time domain and frequency domain real time applications.

As in the diagram below, the talker on the right may speak into the microphone. The speech is captured and transmitted to the remote listener on the left. The left speaker may send back the speech through the remote end microphone to the near end speaker on the right. We would like to cancel the feedback speech before it gets to the near end speaker. The Delay estimation and AEC blocks on the right perform such a function.

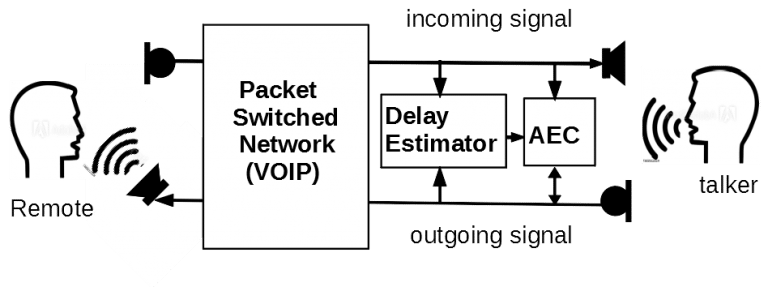
Figure 1 Audio Feedback Through Packet Switched Network

The unit Delay Estimator is usually achieved by performing cross-correlation between the outgoing speech signal incoming signal as shown in the diagram.

Figure 2 Time Delay Estimation

Two signals are said to be fully correlated or coherent when one is the delayed and scaled version of the other. For two sinusoidal signals, this amounts to the fixed-phase relation between the two.

Time domain cross-correlation

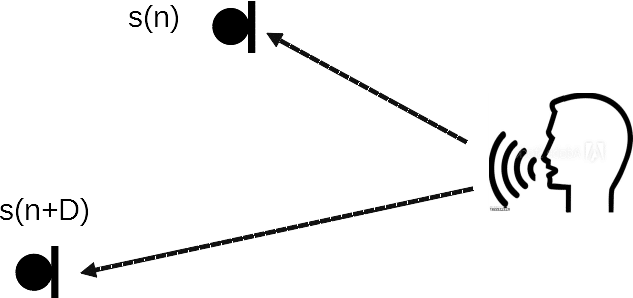
Figure 2 shows a single sound source with two microphones. The sound from the source reaches to the first microphone as x(t) = s(t) and the second microphone y(t) = s(t+D). To estimate the delay D we can use the cross-correlation,

$R_{x,y}(t,t+\tau)= E[x(t)y(t+\tau)]$

and the that gives the maximum value is the estimate of D.

Since we are always limited to a finite observation time, must be estimated. For ergodic processes, this is computed by,

$R_{x,y}(t,t+\tau) = \frac{1}{T-\tau} \int_{\tau}^{T} x(t)y(t+\tau)dt$

where T is the finite observation interval. In practice, the integration is approximated by a summation.

We may also compute the cross correlation from the inverse Fourier transform of the cross spectrum, G_xy (f), as following,

$R_{x,y}(t,t+\tau) = \int_{-\infty}^{\infty} (G_{x,y}(f)e^{j2\pi f\tau} )df$

In order to reduce the error in , and thus improve the accuracy of D, we can pre-filter x(t) and y(t) prior to cross-correlation. The filer would be selected to emphasize frequencies where the signal-to-noise radio is highest and de-emphasize them where it is low.

The cross-spectrum and correlation so filtered are,

$G_{xy} (f)=H_1(f) H_2(f) G_{xy}(f)$

and

$R_{x,y}(t,t+\tau) = \int_{-\infty}^{\infty} (W(f)G_{x,y}(f)e^{j2\pi f\tau} )df$

where W(f) = . This is usually referred to as generalized cross-correlation function.

Complete Communications Engineering

Correlation Techniques