Maximum Directivity Factor (DF) beamforming is a generalized case of the Superdirective beamformer where the desired look direction and the inter-element spacing is small. It was shown in, the Microphone Array Acoustic Beamforming Compromise, that Superdirective, ergo maximum DF beamformers achieve superior spatial selectivity, but result in amplification of uncorrelated noise. In practice, the microphone signal contains a combination of the directional and uncorrelated noise fields. In order to add robustness to the beamforming filter design, both noise models need to be incorporated.
The coherence function of the spherically isotropic noise field is the sinc function. The elements of the coherence matrix, are
, where
is the microphone spacing between mics i and j, and c is the speed of sound. The coherence matrix of an uncorrelated noise field is the identity matrix,
. Therefore, adding these two models together we have,
. To tradeoff between the directivity and WNG, we can introduce a frequency dependent scaling factor, such that
. The robust maximum DF beamforming equation is:
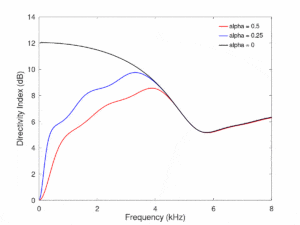
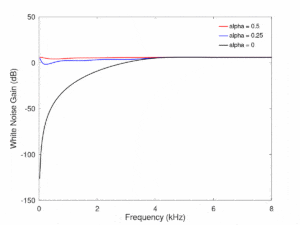
The scaling factor can be made to be a ratio of the estimated sensor noise power to ambient noise power. The figures below show the WNG and Directivity Index metrics for different values of alpha. This setup used a 4-element uniform linear array, which the desired direction in the end-fire direction.
VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task.