A multi-mic noisy signal can be formulated as: $latex<\X_M(t,f)=\ \alpha_MS(t,f)+\beta_MN(t,f)>$, where is the S is the desired (speech) signal, and N is the undesired noise signal, $latex<\\alpha>$ and $latex<\\beta>$ are channel dependent impulse responses of the desired and undesired signals, respectively.
The goal of the Wiener Suppression Rule is to determine the filter that minimizes the error between the estimated speech signal and the actual speech signal. The equation of the Wiener Suppression filter can be written as:
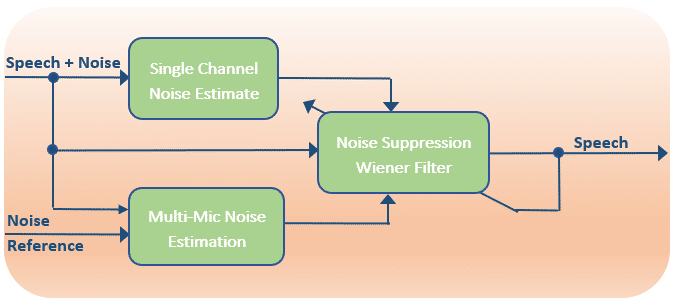
This filter requires information on the signal-to-noise ratio. Most noise reduction algorithms attempting to apply this filter start off by estimating the noise spectrum because this signal is assumed to be more stationary than the desired speech signal. In general, this is true, but noises such as door slams, sirens and keyboard clicks will fail to be attenuated. To help with the noise estimation process a multi-microphone solution can be used.
For example, a dual microphone solution where one microphone is placed near the desired sound source, and a second placed out of acoustic view of the desired signal can be used as an instantaneous estimate of the noise. All that is left to estimate is the transfer function of the noise between the 1st and 2nd microphones. This multi-mic noise estimate can be used to aid the single channel noise estimation. Alternatively, an instantaneous noise estimate can be obtained by applying a nullforming spatial filter to a microphone array in the desired look direction. The difference in power between the original input signal and the nullforming output will also provide some information on the desired speech signal.
VOCAL Technologies offers custom designed multi-mic signal processing solutions to provide superior voice quality. Our custom implementations of such systems are meant to deliver optimum performance for your specific signal processing task.