A linear microphone array, as the name suggests, is set of component microphones that are aligned along a straight line in positions. The following diagram shows a setup of a linear array with three microphones.
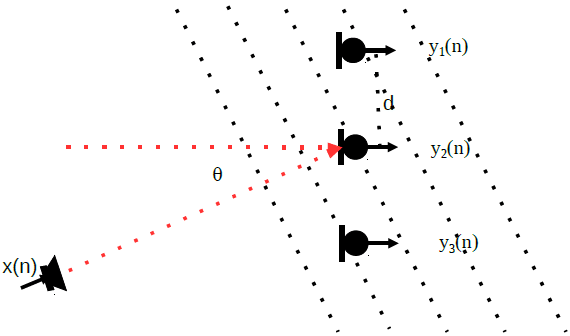
A sound source, x(n), creates a sound field around the neighborhood of the microphone array. We assume far-field model. The sound wave travels perpendicular to the traveling direction at an angle q to the broadside direction of the linear array. The distance between the adjacent component microphones is d.
By measuring the relative delays of the sound wave reaching each microphone, we can calculate the incoming angle of the sound wave. Therefore, we can generate beam pattern spatially selective to enhance the sound from the desired direction and suppress the sound from other directions. This ability to select spatially in a sound field is the main motivation for using microphone arrays.
If it is possible to train the system, we can send out a probe sound from the microphone and the relative delay can be measured by performing cross-correlation of the received sound signals at the component microphones. The angle can be derived after some simple mathematics.
$latex \Theta$ = arcsine ( Δτ * v / d)
where Δτ is the calculated delay for two adjacent microphones, v is the speed of sound and d is the inter-microphone distance. For spherical propagation model, the mathematics becomes more involved, however, the same principle follows.
Linear array beamforming makes use of the derived or prior knowledge of the target sound direction to enhance gain in the target direction. The below links lead to several different approaches VOCAL have researched and tested on practical applications.
More Information
- Minimum Variance Distortionless Response (MVDR) Beamformer
- Linearly Constrained Minimum Variance Beamformer
- Adaptive Steering
- Adaptive Nulling