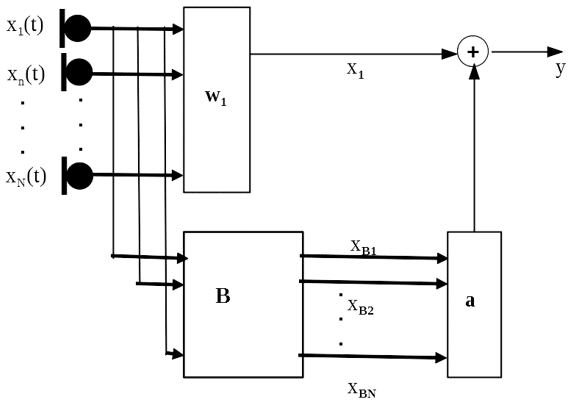
Generalized Sidelobe Canceler (GSC)

Generalized Sidelobe Canceler can be considered as a special case of Linear constrained Minimum Variance (LCMV) beamforming. It is one of the early beamforming approaches in practice.

For LCMV, we formulate the linear constraints as below,

$C^Tw\left(p\right) = c$

where c is the desired vector derived from the priori knowledge of the target source and C denotes a linear matrix which forces ${w}(p)$ into the desired vector c. Obviously ${w}\left(p\right)\$ may not be unique. A commonly chosen solution is

${w}_{1}=C\left(C^TC\right)^{-1}c$ ,

where ${w}_1$ is the minimum L₂-norm solution. It is also referred to as the fixed beamformer.

With this fixed beamformer, we convert the original linearly constrained beamforming problem into a dimension-reduced optimization problem.

Let S be the subspace that defined as

$S=\{v\in R^{ML\times1}:C^Tv=0\}$

and

$C^TB = 0$ ,

$rank\left(B\right) = ML - C$

we call B, the blocking matrix. Obviously, B is not unique. The following combination expands the entire beamforming space,

${w} = {w}_1 + B(a)\left(p\right)$

and

$C^T{w} = {c}$ .

Therefore, the linear constraint imposed on LCMV is observed into the optimization objective function.

${{\underset{{a}\left({p}\right)}{min}}{\left({w}_1+B{a}\left(p\right)\right)}}^TR{{xx}}\left({w}_1+B{a}\left(p\right)\right)$

Now the problem can be easily solved with the standard Wiener solution,

${{a}}=-{R}_{{x}_{B}{x}_{B}}^{-{1}}{{E}}\{{x}_{1}{x}_{B}\left({p}\right)\}$

The implementation can be naturally carried out in an iterative fashion. The involved computation is equivalent to the LCMV since B and ${w}_1$ are both pre-calculated.

Complete Communications Engineering