Signal restoration (or signal de-noising) processing has similar objective to noise suppression or noise reduction processing. Signal restoration has been typically understood as an off-line processing. Advanced signal restoration and signal de-noising consumes significant amount of processing power and this used to make such applications often prohibitive from the viewpoint of real-time embedded signal processing.
In signal restoration the bandwidth is often pre-determined and relatively wide when comparing to Telephony applications, for example. When working in “traditional” signal restoration it is common to de-noise signals having Fs of 48kHz or 44.1kHz. Thus it is expected that the required processing power is much greater than in the case of typical real-time DSP tasks associated with Speech Enhancement for Telecommunication applications (either in Digital TDM Telephony, in Voice-over-IP Telephony or in Cellular Telephony). With DSP engines being faster and more efficient, the signal restoration using more advanced processing techniques can be done by embedded DSP-based systems in real-time.
The signal restoration method and algorithm operate as follows (cf.[1]):
Step 0: Initialization; the signal estimate (i.e., the restored signal) xo is set to the input signal y (the input is a sum of the original signal and noise), both signals/vectors are extended over the projection time segment length of P. In the model case the noise is assumed to be Gaussian and white, in practice these assumptions are often compromised and thus the final result may differ from the predicted result.
Iterations for i=0,1,… , as per the following steps (Steps 1 through 6):
Step 1: Estimate the predictor parameter vector ai, as per the linear prediction method:
Step 2: Calculate an estimate of the model gain using the Parseval’s formula;
Step 3: Calculate an estimate of the power spectrum of speech model, as per the Linear Prediction;
Step 4: Calculate the Wiener filter frequency response;
Step 5: Filter the magnitude spectrum of the noisy speech signal;
Step 6: Go to Step 1 until condition for convergence is met (or until the number of iterations is attained) as per the convergence pre-defined requirements. Otherwise, exit the iteration loop
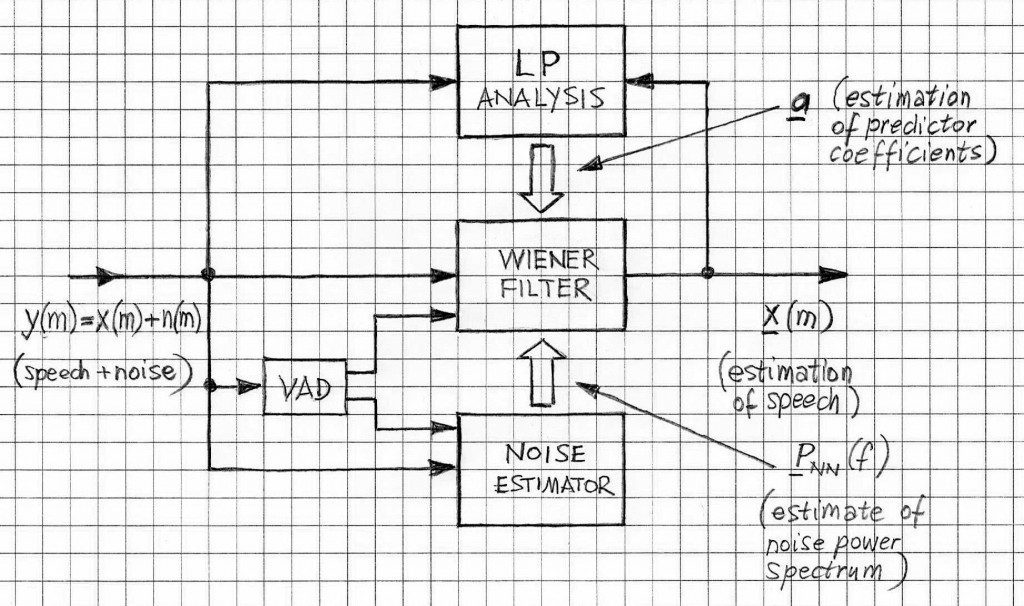
Figure 1 illustrates the signal restoration process. In fact the block diagram resembles the block diagram of the Spectral Subtraction (SS). Yet the differences are profound. In the original SS there is no iteration process and there is no prediction analysis. In this sense, these two approaches are very different, despite apparent similarities.
VOCAL’s Speech Enhancement solutions have been deployed worldwide. These solutions are portable to any typical digital signal processor or general-purpose processor. The Voice Enhancement solutions can include custom add-on components such as Frequency-Domain Signal Restoration using Prediction Filtering. Contact us to discuss your requirements with our engineering staff.
More Information
References
- Linear Prediction Models (Chapter 8), in Advanced Signal Processing and Noise, by Vaseghi, S.V., 2nd Edition, John Wiley & Sons, 2000