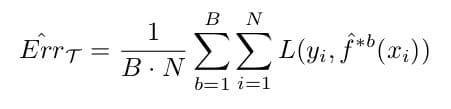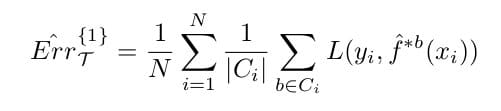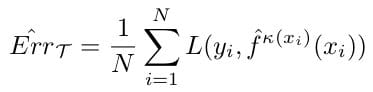VOCAL has developed extensive model validation software to assure your Voice Activity Detection solution is optimal. With over 20 years of collected data, we have available a unique, vast, and detailed landscape from which to understand your problem and provide the best possible analysis. Contact us to discuss your voice application requirements.
Model Assessment and Validation
When trying to determine the predictive model to use, we need to determine which models represent an accurate description of the phenomena, and which models are best to generalize to new data. To do so, we perform model assessment, which are techniques to measure the prediction, also known as the generalization or test error, for the models. For a classification problem, the test error is defined as:
Where G is the true class, Ĝ(X) is the class estimate given predictor set X and Τ is the dataset we are using to create X with which to train the classifier. A loss function L is:
Where I is the indicator function, and is known as 0-1 loss. The three most effective techniques in model assessment are the Split-Data Method, the Bootstrap, and K-Folds Cross Validation.
The Split-Data Method
The Split-Data Method is suited for both Validation and Testing, is perhaps the most conceptually simple of the three methods, and appropriate when you are awash in data. Essentially, the technique is to split the data into three mutually exclusive categories as follows:
Split-Data Subsets [1]
As the relative proportions suggest, Training should be done over about half the data set, while the next two quarters should be reserved for Validation and Testing respectively. When we say Validation, we mean assessing whether or not the model accurately describes reality, in order to choose amongst the different models. Once this is done, we measure the validated model against the new test data. It should be noted that the Training stage must never see data belonging to the Validation and Test stages of the approach.
The Bootstrap
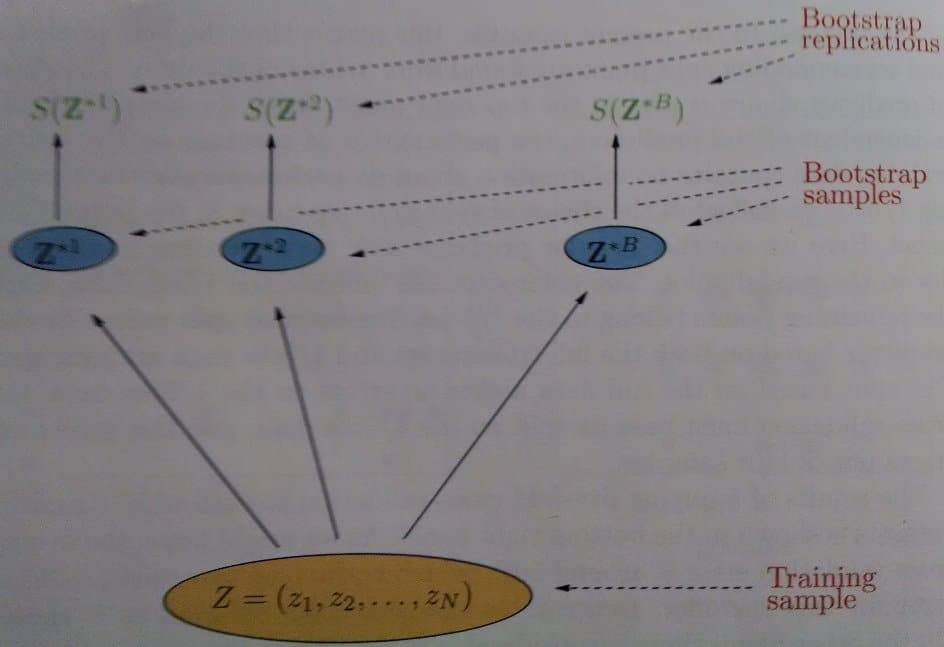
Often times, we do not have enough data to go about performing Validation and Testing in such a manner. When we are hard pressed for data, we can use the Bootstrap technique to perform model selection through Validation. It is well suited for model selection because it has a low variance. Essentially, we wish to estimate our test error by first randomly sampling from the training set with replacement B times, to generate B bootstrap training sets. We fit our model to each b ϵ B, and examine L across these bootstrapped sets. A diagram is shown below:
Bootstrap Technique [1]
Where S(Z*b) is the bth estimate of our statistical quantity, in this case, ErrΤ. If we denote ḟ *b(xi) as the value of xi predicted by bootstrap model b, the test error estimate is:
Unfortunately, this is actually an overly optimistic test error estimate, because the test set and the training set inevitably overlap. To solve this problem, we introduce the Leave-One-Out Bootstrap, which, for each observation xi, keeps track of predictors from bootstrapped data not containing this current observation. It can be expressed as:
Where |Ci| is the size of the set of indices of bootstrap samples that do not contain the current observation xi. Obviously, Ci ≠ ø, else we simply throw away such terms, as the above is only an estimate. This solves the previous problem, but unfortunately still exhibits training-set-size bias, since |Ci| is dependent on the size of the dataset.
K-Fold Cross Validation
When data is scarce for testing, we can use k-fold cross validation to replace the test split, and therefore provide a final estimate of our final model chosen via bootstrap. In K-Fold Cross Validation, we first split the data up into K groups, known as cross validation folds, in a stratified manner across classes. That is, we are sure to select the same amount of data, albeit randomly, from each class, for each fold. Then for each individual fold K, we screen the predictor set for a subset of good predictors that exhibit strong univariate correlation with the classes, low mutual information, and minimal maximum pairwise correlation using all the samples except those in the current fold k. Then, using just this filtered subset, we train our classifier on all samples except on those in the current fold k. We then use the current fold as the test set to predict on, and compute our loss function. We then average the loss function across folds. A diagram is shown below:
K-Fold Cross Validation Technique [1]
Therefore, given ƙ : Τ → Ƙ which maps our training data Τ into a partition ƙ, we denote ḟ ƙ(xi)(xi) be the predicted value given observation xi, we denote our cross-validation generalization error as:
Typically, K is chosen to be 5 or 10. This is to control the bias-variance tradeoff, which is inevitable in any predictive model, but may be negligible for certain models and certainly for large datasets. When the number of samples is low, cross validation results in high bias, no matter what we choose for K. In general however, low values of K, such as 2 or 3, have higher bias than higher values. Since the model must be completely retrained for each fold, a high number of folds may become computationally prohibitive, although in currently this has become less and less of an issue.
Generally, this method has a higher variance than other methods. To mitigate this, simply repeat the cross-validation procedure many times to reduce this variance. By averaging the results, we can reduce variance and keep the small bias associated with the current value of K.
Recommendations for Classification Model Selection
There are a few common sense rules of thumb for performing model selection [2]:
- For the Split-Data Method, the test set should be no less than 20% of the entire dataset.
- In general, the bigger the proportion of data used for the test set, the smaller your standard errors, but this comes at the expense of an increased bias because we are using less data to train.
- We need to be aware that there exists optimization bias, which is the result of tuning the model parameters using a resampling scheme instead of a dedicated test set.
- Therefore, when possible, estimate the model’s tuning parameters using a dedicated test set and save the resampling methods for estimating test error. In addition, any unsupervised predictor screening, such as selecting the subset of predictors with the highest variance, should be done across the entire data set, not within a fold or a bootstrap dataset.
- When choosing a model to use, start with the most complex, most general, and least interpretable first. Next, pick a less general and more interpretable model. Keep reducing the complexity while increasing the interpretability until the performance becomes unacceptable. This will allow you to understand the performance ceiling of your dataset and your chosen predictors, and give you insight on the validity of your understanding of the problem.
- Following Occam’s Razor, simpler models with the same performance are always preferred because they are more interpretable. Therefore, a standard technique is One-Standard-Error selection, which finds the numerically optimal model, and then chooses as the final model the simplest one within one standard error. Alternatively, you could pick the simplest model within p% of this globally optimal solution.
- Always characterize your errors. When you can reliably estimate their distribution, you can use statistically optimal hypothesis tests to determine which models are significantly different from each other.
- For instance, in the case of standard normal errors, the paired t-test is the preferred statistical hypothesis test.
More Information
References
[1] T. Hastie, R. Tibshirani, J. Friedman, Elements of Statistical Learning: Data Mining, Inference, and Prediction , 2nd ed. New York, NY: Springer, 2009.
[2] M. Kuhn, K. Johnson, Applied Predictive Modeling , 1st ed. New York, NY: Springer, 2013.