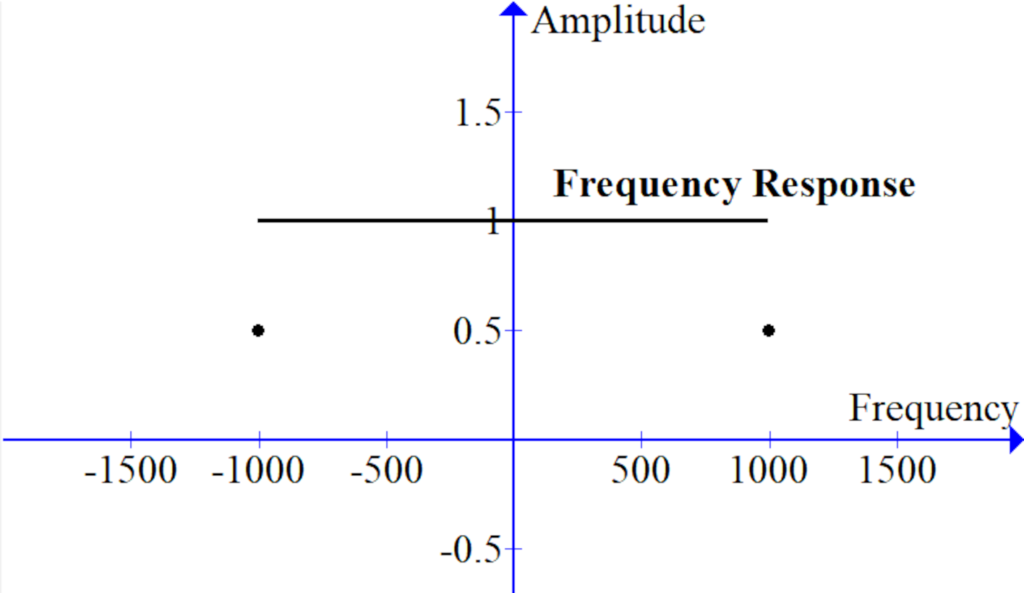
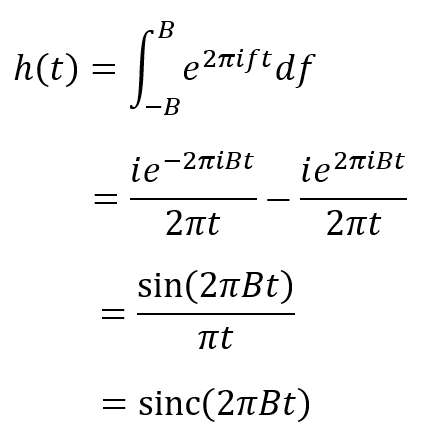A sinc filter is a type of low-pass filter. The mathematical basis for the sinc filter is a ‘perfect’ low pass filter with a cutoff frequency. Components of the signal with frequencies less than the cutoff are let through unaffected, while components with higher frequencies are completely removed. The frequency domain response of an ideal sinc filter is a rectangular function, as illustrated below:
One way to implement a sinc filter is as a finite impulse response (FIR) filter. In this type of filter, a block of coefficients is convoluted with a block of input samples to produce one output sample. The coefficients can be calculated from the inverse Fourier transform of the frequency domain response. For the sync filter, this calculation is as follows:
This equation shows that each coefficient is calculated using the sinc function, which is where the filter gets its name. The constant B is the cutoff frequency. We can calculate the filter coefficients using this time-domain expression with seconds as the unit of time and Hertz (1 / s) as the unit of frequency. When applying the filter, each coefficient will be applied to one sample, so the duration of each coefficient is the same as the duration of an audio sample. After calculating the coefficients, they should be normalized so their sum is 1. This will ensure that the filter does not introduce any gain to the signal. The following source code shows an example implementation of a sinc filter:
#include <stdio.h> #include <math.h> #include <float.h> #include <stdint.h>
#define WINDOW_SIZE 64 #define SAMPLE_RATE 8000 #define CUTOFF_FREQUENCY 700
double sinc (double x) { if (x == 0.0) { return 1.0; } return sin(x) / x; }
int main (int argc, char *argv[]) { int i, ai, ci; double coef[2 * WINDOW_SIZE]; double abuf[WINDOW_SIZE] = {0}; double const_2b = 2.0 * (double)CUTOFF_FREQUENCY; double dx = const_2b / (double)SAMPLE_RATE; double x, g, cs; FILE *fin, *fout; int16_t si, fsi; double s, fs;
if (argc < 3) { printf(“More args please\n”); return 0; }
/* Generate the filter coefficients */ g = 0.0; x = -(dx * (double)(WINDOW_SIZE – 1)) / 2.0; for (i = 0; i < WINDOW_SIZE; i++, x += dx) { coef[i] = sinc(M_PI * x); g += coef[i]; } cs = 1.0 / g; for (i = 0; i < WINDOW_SIZE; i++) { coef[i] *= cs; coef[i + WINDOW_SIZE] = coef[i]; }
/* Open files */ fin = fopen(argv[1], “rb”); fout = fopen(argv[2], “wb”);
/* Apply the filter to the input file and generate an output file */ ai = 0; ci = WINDOW_SIZE – 1; while (1) {
/* Read the next sample and store it in a circular buffer */ if (fread(&si, 2, 1, fin) != 1) { break; } s = (double)si / 32768.0; abuf[ai++] = s; if (ai >= WINDOW_SIZE) { ai = 0; }
/* Compute the convolution and update the window position */ fs = 0.0; for (i = 0; i < WINDOW_SIZE; i++) { fs += abuf[i] * coef[ci + i]; } ci–; if (ci <= 0) { ci = WINDOW_SIZE – 1; }
/* Write the output sample */ fs *= 32768.0; if (fs > 32767.0) { fs = 32767.0; } else if (fs < –32768.0) { fs = –32768.0; } fsi = (int16_t)fs; fwrite(&fsi, 2, 1, fout); }
return 0; } |