Musical Noise in Acoustic Noise Reduction

I. What is Musical Noise?

Musical noise is a perceptual phenomena that occurs when isolated peaks are left in a spectrum after processing with a spectral subtraction type algorithm. In speech absent sections of a signal, these isolated components sound like musical tones to our ears. In speech present sections, it produces an audible ’warble’ of the speech. A nice illustration of musical noise is given below:

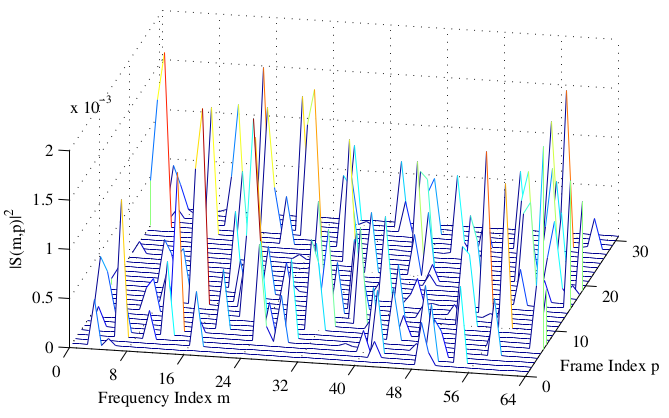
As illustrated above, these peaks are often much larger than the surrounding energy. This is true in both noise only and speech present sections. It is this great discrepancy in magnitude between pairs of frequency bins that causes the musical noise phenomena. The higher the peaks relative to the surroundings, the worse the musical noise. You can see musical noise present in the spectrogram below:

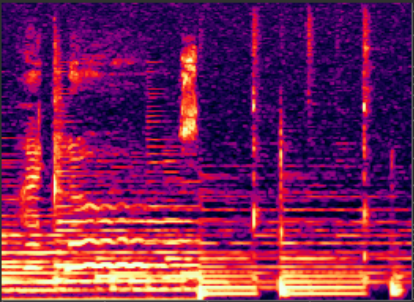
In a spectrogram, musical noise presents itself as a random speckling of color. You can see these random and unconnected peaks especially clearly in the high frequencies near the top of the figure. Instead of being either uniformly dark, or uniformly colored, the musical noise corrupted spectrogram appears grainy via the random dots of color representing the randomly distributed energy.

II. Controlling Musical Noise

Throughout the years, there have been many ways to control the amount of musical noise created after spectral subtraction. Since musical noise is inherently a product of the variance in the spectral estimates, the most obvious approach is to use a smoothed version of the incoming spectra to create the noise estimator. While this does reduce the amount of musical noise, it does not eliminate it, and the spectrum can only be made so smooth before other distortions start creeping in. Here we will consider other approaches that can be used in tandem to spectral smoothing.

Parametric Spectral Subtraction

One of the most effective and perceptually pleasing ways to reduce musical noise is by parameterizing standard spectral subtraction. In parametric spectral subtraction, we introduce α and β as the oversubtraction, and spectral flooring parameters respectively. They can be incorporated into the magnitude spectral subtraction model as follows:

(1)

Where Ŝ[m,k] is the fourier transform of the clean speech estimate at frame m and frequency bin k, Y represents the input speech spectrum, and Ê represents the estimated noise energy. As you can see from above, α determines how much to subtract from the noisy signal, hence it is called the oversubtraction parameter. If we subtract too little, then the speech will still be noisy, but if we subtract too much then we will get those dreaded isolated peaks across frames resulting in unwanted musical noise.

Thankfully, this musical noise can be masked by the second condition using β. If we subtract too much, instead of half-wave rectifying the result as is normally done in spectral subtraction, we simply set the resulting frames energy to a noise floor. This noise floor is meant to mask the musical noise, but as the above shows, too high of a floor will result in too much noise energy being present and thus a noisy speech frame results.

Clearly, these parameters need to be tuned. Various authors have suggested bounds, but ultimately it is up to the designer to select the parameters such that the resulting signal is perceptually pleasing. Musical noise is highly objectionable as it is a synthetic result, and so it is often preferable to retain more of the natural noise by setting a higher floor and erring on the side of subtracting too little when this is the only method employed. When musical noise is still present after spectral smoothing and parametric tuning, we can turn to post-processing solutions for further musical noise reduction.

Musical Noise Filtering

One of the most efficient approaches for musical noise reduction is the addition of a postfilter for adaptive spectral smoothing. In this model, speech presence or absence needs to be estimated for the current frame, and based on this estimate a window is derived to filter the gain function thereby reducing musical noise. The strength of this method is the gain smoothing being proportional to the SNR of the frame. Lower SNR frames experience more smoothing and hence experience more postfilter compensation for the  increased amount of subtraction. The block diagram of this method is shown below:

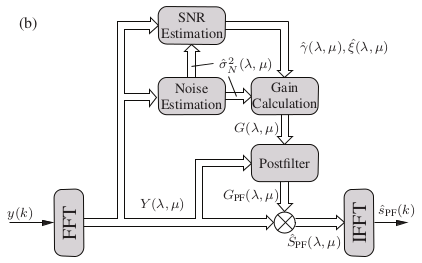
We use the following to estimate the probability of speech in the current frame:

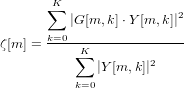(2)

Where G is the gain factor, defined as:

(3)

ζ is then thresholded to determine the probability of speech present, and provide the designer a level of control over the amount of musical noise reduction and smoothing distortion:

(4)

Now we can define our postfilter as a rectangular window:

(5)

Where N[m] is the length of the window for the current frame found via:

(6)

Where ⌈⋅⌋ represents rounding to the nearest integer, and ψ is a scaling factor that sets the length order of magnitude and hence determines the maximum post-filter smoothing. The gain function is then modified as:

(7)

Since we are convolving with a rectangular window in the frequency domain, we are essentially low pass filtering the gains in the time domain. Another way to look at it is that we are weighting the time domain impulse response of an ideal low pass filter in the time domain with the spectral subtractive gain function. The length of this window, and hence the low pass cut-off frequency and thus the degree of frequency gain smoothing is dependent on the SNR. For long window lengths, we have high cut off frequencies, and thus less smoothing. For shorter window lengths, we will perform more smoothing. The degree of smoothing is essentially dictated by ψ, and hence mostly up to the designer.

Convolution is considered a relatively expensive operation. For long window lengths, this is especially true. It is well known that convolution in one domain corresponds to multiplication with the fourier dual. Therefore, this convolution can be efficiently calculated for long window lengths by multiplication using their fourier duals.

III. Other Improvements

Besides the addition of a post filter, there are a few small things that we can do to the parametric spectral subtraction algorithm to decrease musical noise. In this section, we will consider them one at a time. These solutions are the simplest to implement, but taken together can result in significant improvements in musical noise reduction.

Adaptive Frequency Selective Smoothed Oversubtraction

Due to the masking properties of the human ear, musical noise at one frequency may be more noticeable than at another. Indeed, our ears tend to be more sensitive to low and mid spectrum distortions than those at high frequencies. To model this effect, we can divide our frequency spectrum into constant Q also known as octave bands, and change the oversubtraction factor based on the calculated statistics in that band. We can make this more precise by using third octave bands. If 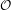= 0,…,O − 1 are our third octave bands, the center frequency (Hz) of the oth third octave filter bank is given by [4]:

(8)

Where the upper and lower band limits are given respectively by:

This can be efficiently implemented by performing the filter bank deconstruction directly in the frequency domain [5]. To do this, we must first design our time domain window w. Often a good choice is the Hamming window, created to be centered at the band center frequency. The time domain Hamming window for the oth band is then:

(11)

Again, instead of convolution, we use frequency domain multiplication. That is we let 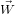= 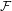(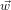) and create the oth band via:

(12)

Where Y is the discrete fourier transform of the noisy input signal, k is the discrete frequency index, (⋅)^⋆ denotes complex conjugation. This approach clearly favors high resolution FFTs as the advantage of this method over simple convolution becomes greater as the resolution of the FFT increases, but is still an efficient procedure for the perceptually important filter lengths usually used in audio processing. For each band o per frame m, we can calculate the per-band SNR denoted simply as SNR here for simplicity of notation and use that adaptively modify the oversubtraction factor alpha. We modify α as [6]:

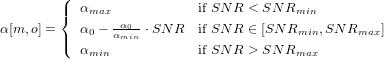(13)

Where α₀ is the subtraction factor at an SNR of 0, α_min is the minimum oversubtraction factor at SNR_min, and α_max is the maximum oversubtraction factor at SNR_max. These parameters are tunable and are hence up to the designer of the algorithm. In some environments, the oversubtraction factor may change abruptly across bands. To correct for this, we can smooth α across the bands using simple least squares smoothing. Alternatively, we can use these factors to reconstruct the gain function across FFT frequency bins, and let the post-filter handle the smoothing.

Whitening with Tapering

We can create a final post-process to filter the data before being sent out. This final process is a whitening and tapering of the full frequency spectrum that exploits the psychophysical perceptual qualities of our auditory system. In essence, our ears do well in discriminating sounds in white noise versus colored noise, and are more sensitive to low and mid range frequencies than high frequencies. To exploit this, we first need to whiten the post-filtered spectrum Ŝ_PF:

(14)

Where b is the degree of whitening. When b = 0 we use no whitening, and when b = 1 the spectrum is fully whitened. This is simply dividing the spectrum elementwise by a factor of the maximum spectral amplitude in the frame. The next thing to do is to smoothly taper off the high frequency components. This can be done by multiplication with the right half of the hamming window:

(15)

Of course, there are other choices of tapering functions we can use that will change tapered -3dB frequency. The result of the whitening and tapering procedure is a perceptually pleasing noise spectrum which masks the musical noise we are trying to avoid. Combined with the octave band post-filtering procedure in a parametric spectral subtraction algorithm, musical noise can be effectively eliminated.

More Information

• Voice Enhancement Design
• Octave Banks for Acoustic Filtering

References