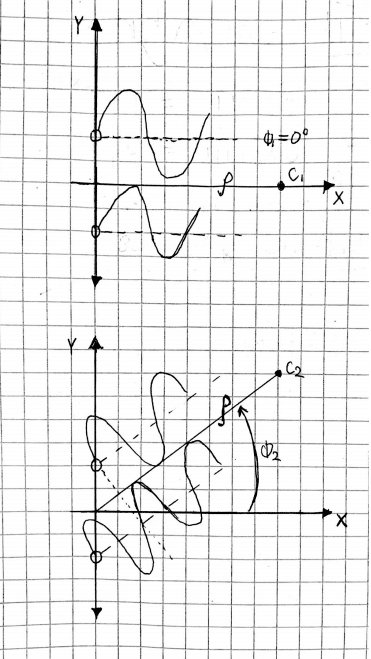For a microphone array arrangement, spatial aliasing occurs when the source signal phase difference in two different directions is equal. That is, two different directions which should be otherwise unique are indistinguishable from each other when spatial aliasing occurs. The far-field model requires that the sensors in the array are arranged at a certain distance from each other so that aliasing does not occur. This concept is similar to Nyquist’s theorem for sampling signals, except that in this case the aliasing occurs due to the spatial geometry of the model.
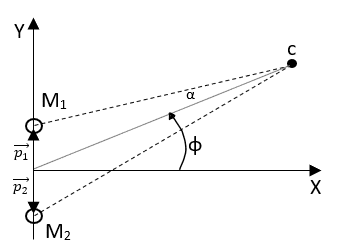
Consider the far-field model where ρ is the distance from the point source to the center of the coordinate system, and is the direction of the point source relative to the horizontal axis.
Figure 1: Far–Field Sound Capture Model
The captured signal from each microphone in the array is given in the frequency domain as:
(1.1)
The phase rotation and decay due to distance vector for the far-field model can be denoted as:
(1.2)
Therefore, if there exists two unique angles such that eq. 1.3 is true, spatial aliasing will occur.
(1.3)
When spatial aliasing occurs, the direction of arrival of the signal is ambiguous. An example of spatial aliasing is illustrated in Figure 2, where two signals from different angles have the same phase difference, and are therefore indistinguishable from each other. To prevent spatial aliasing, the distance between the two microphones must be smaller than half a wavelength of the highest frequency in the signal.
Figure 2: Spatial Aliasing Diagram