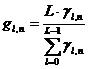Proportionate Normalized Least Mean Squares Adaptation

Continuous effort to improve the convergence speed and reduce complexity of adaptive filters resulted in several improvements of the NLMS algorithm. While the essence of the NLMS algorithm has virtually remained intact, the improvements, particularly in applications to Line/Network Echo Cancellation (LEC/NEC) have been substantial and they have been tested in real-world scenarios.

Since the NLMS algorithm is known as the least expensive adaptation algorithm, algorithm improvement and implementation refinement activities have been focused to a great extent on this algorithm. The Proportionate Normalized Least Mean Squares (PNLMS) algorithm is one of the notable results of this effort.

The first paper on PNLMS was published in 2000, Ref.[1]. However, earlier papers in the area of LMS improvements signaled merits of the basic concept of using the step size adjusted to individual taps of the adaptive FIR filter, on which the PNLMS algorithm is based, cf. Refs.[2],[3].

In the NLMS adaptation the adaptation step size is defined as a scalar constant. In PNLMS adaptation, the adaptation step size is proportional to a vector G_n=diag[g_0,n, g_1,n ,…,g_L-1,n] of the size of the FIR adaptive filter length L whose elements vary. At each tap position individual elements of vector G_n vary from position to position and are proportional (approximately) at each tap position to the absolute value of the current adaptive filter tap weight estimate.  In other words, unlike in the case of the NLMS, the adaptation “energy” in the PNLMS algorithm  is distributed unevenly over the L taps: the more “energy” the given filter coefficient carries, the more adaptation weight is applied to it (cf. Ref. [1]).

The PNLMS algorithm is described by the following adaption formula:

                                                                                             (1)

in which

G_n=diag[g_0,n, g_1,n ,…,g_L-1,n]                                                                                                      (2)

x_n=[x_n, x_n-1,…,x_n-L+1]T                                                                                                              (3)

                                                                                                                                 (4)

G_n is a diagonal matrix which defines the step sizes of the individual taps of the adaptive filter, μ is overall step-size parameter and δ is a protection parameter (usually very small) preventing Formula (1) from being singular.

The elements of the matrix are calculated as per (5) and (6), namely:

                                                                                                                                        (5)

In which γ_l,n are defined as follows:

 , 0 ≤ l ≤ L-1                                 (6)

Parameters δ_p and ρ are positive numbers chosen heuristically.

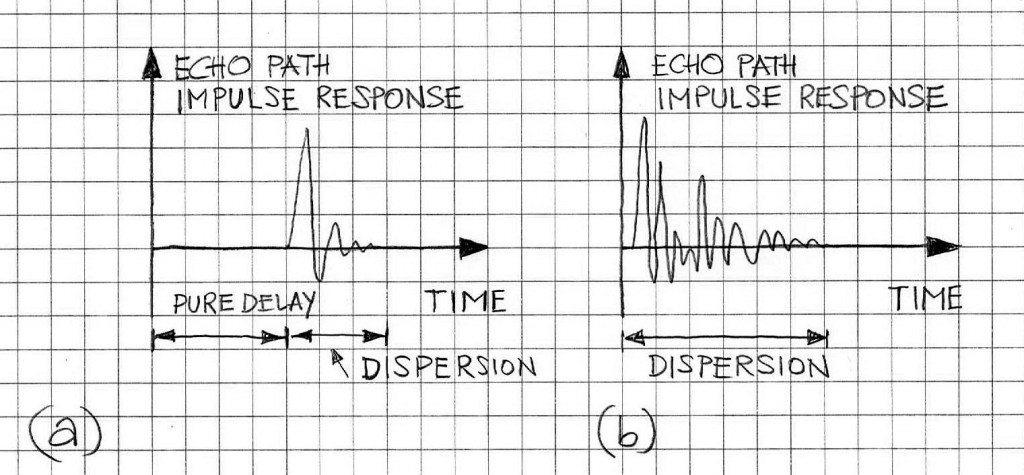
A closer look into the PNLMS algorithm reveals that its performance greatly depends on the types of the echo paths (cf. Figure 1). The true benefits of using the PNLMS algorithm (faster convergence) are achieved when echo paths are sparse. Therefore, predominant applications of PNLMS algorithms are in Line/Network echo cancellers (LEC/NEC), as the typical hybrid-related echo paths are sparse. Otherwise, for dispersive echo paths (typically observed in acoustical environment) there are hardly any tangible benefits from the viewpoint of the algorithm convergence speed.

In terms of computation cost associated with implementing the PNLMS algorithm, the general formula, O(L) remains intact. However, there is a multiplicative factor that indicates that the computation cost is slightly greater than in the case of the NLMS algorithm using the same length of the FIR filter.

VOCAL’s implementations of the echo cancellation designs are based on the full-band and sub-band NLMS adaptive algorithm. If sparse echo paths are anticipated in the given application, VOCAL Technologies has custom solutions that can be considered for use. The PNLMS is one of them, and it can be added as a custom offering, if required. Contact us to discuss your echo cancellation application with our engineering staff.

More Information

• Echo Cancellation Design
• Speech Enhancement Design

References

1. D. L. Duttweiler, “Proportionate normalized least-mean-squares adaptation in echo cancelers,” IEEE Trans. Speech and Audio Processing, vol. 8, no. 5, pp. 508–518, Sept. 2000.
2. D. L. Duttweiler, “Subsampling to estimate delay with application to echo cancelling,” IEEE Trans. Acoustics, Speech, Signal Processing, vol. 31, pp. 1090–1099, Oct. 1983.
3. J. B. Evans, P. Xue, and B. Liu, “Analysis and implementation of variable step-size adaptive algorithms,” IEEE Trans. Acoust., Speech, Signal Processing, vol. 41, Aug. 1993.
4. H. Deng and M. Doroslovacki, “Improving convergence of the PNLMS algorithm for sparse impulse response identification,” IEEE Signal Processing Letters, vol. 12, no. 3, pp. 181–184, Mar. 2005.
5. R. K. Martin, W. A. Sethares, R. C. Williamson, and C. R. J. Jr., “Exploiting sparsity in adaptive filters,” IEEE Trans. Signal Processing, vol. 50, no. 8, pp. 1883–1894, Aug. 2002.
6. S. Kawamura and M. Hatori, “A tap selection algorithm for adaptive filters,” in Proc. IEEE Int. Conf. on Acoustics, Speech, Signal Processing, Apr. 1986, pp. 2979–2982.
7. K. C. Ho and S. D. Blunt, “Rapid identification of a sparse impulse response using an adaptive algorithm in the Haar domain,” IEEE Trans. Signal Processing, vol. 51, no. 3, pp. 628–638, Mar. 2003.
8. J. Cui, P. A. Naylor, and D. T. Brown, “An improved IPNLMS algorithm for echo cancellation in packet-switched networks,” in Proc. IEEE Int. Conf. on Acoustics, Speech, Signal Processing, vol. 4, May 2004, pp. 141–144
9. J. Benesty and S. L. Gay, “An improved PNLMS algorithm,” in Proc. IEEE Int. Conf. on Acoustics, Speech, Signal Processing, vol. 2, May 2002, pp. 1881–1884.