This note is a version of a note entitled “ON POTENTIAL INSTABILITY OF NE/FE SYSTEM WITHOUT ECHO CANCELLATION” and it can be used as a reference. Herein echo cancellers to both ends of the Near-End/Far-End system have been added. It is not of great importance for the stability analysis whether the echo cancellers are Line/Network Echo Cancellers or Acoustic Echo Cancellers. Figure 1 depicts the overall system. In order to extract TX and RX signals from the 2-wire links, ideal secondary hybrid circuits have been added. They do not play a role in the system stability analysis.
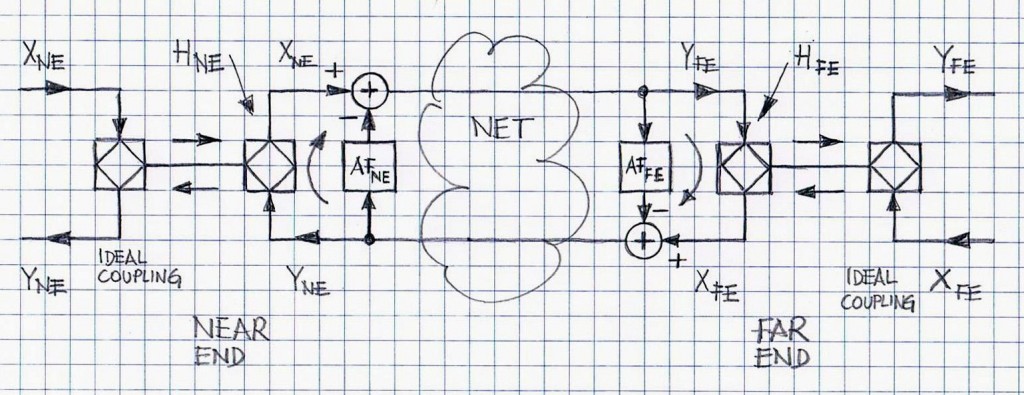
As explained in the referenced note the Near-End/Far-End system terminated with either hybrid circuits or acoustic echo paths is potentially unstable. By adding echo cancellers, no substantial changes to the potential instability are made.
To facilitate the system analysis the network delays have been ignored. A simplified block diagram is depicted in Figure 2.
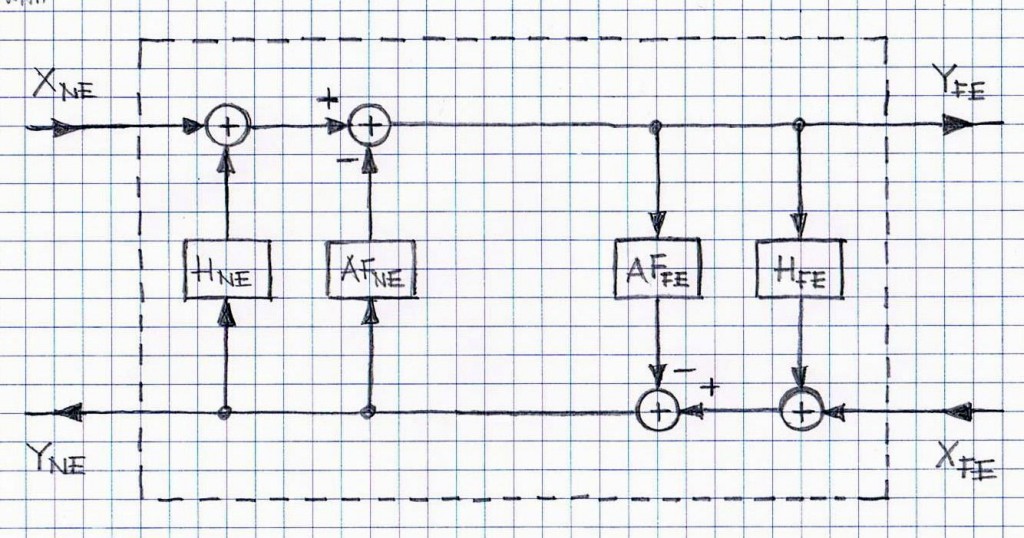
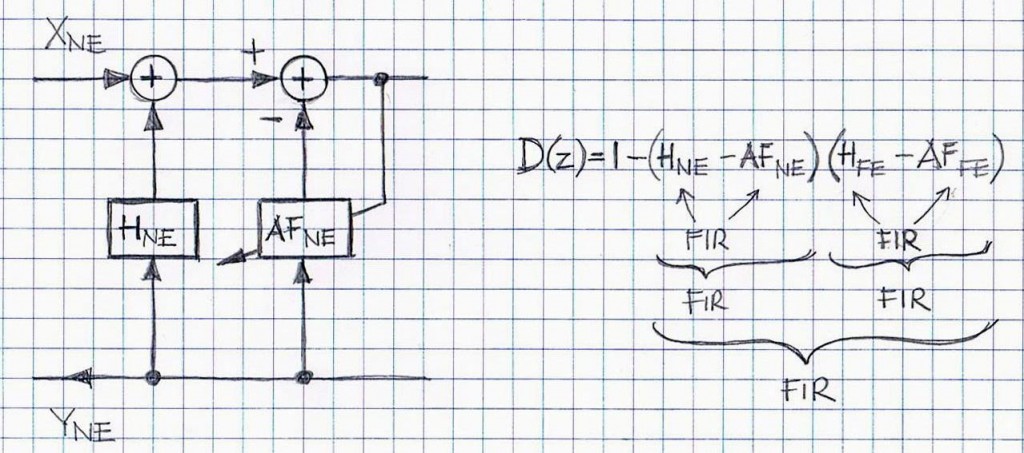
In order to reuse the analysis outlined in the referenced note “ON POTENTIAL INSTABILITY OF NE/FE SYSTEM WITHOUT ECHO CANCELLATION”, it is sufficient to substitute HNE(z) and HFE(z) with HNE(z) = HNE(z) – AFNE(z) and HFE(z) = HFE(z) – AFFE(z), respectively. Figure 3 provides an additional explanation for that substitution.
Using the same notation as in the referenced note, we can express the system transfer function matrix T as in Y = T . X, where the input is X = col[XNE , XFE] and the output is Y = col [YNE , YFE], and with the transfer function matrix T comprising of {Tij}, i,j = 1,2, as below:
where all quantities as expressed as z-transforms of the respective sampled quantities.
Eventually we arrive at:
where:
Assuming that both echo paths/echo transfer functions (i.e., HNE(z) and HFE(z) ) are of FIR type as well as AF filters are of FIR as well, we notice that all {Tij}, i,j = 1,2, are of IIR type and their inherent instability comes from zeroes of D(z) (as per Eq.3).
Note that in the above analysis, other sub-blocks of the echo canceller were ignored for two reasons: (i) to focus on the root cause of the system instability and (ii) to simplify the analysis and limit it only to the linear model of the system with echo cancellers/adaptive filters.
In fact, sub-blocks such as NLP and DTD play role in specific modes of system instability. They also are used, with other functional blocks of ECAN, to mitigate or control system instability.
The potential instability of the Near/End-Far/End voice channel system equipped could be effectively controlled by anti-instability feature within the echo canceller. Well-designed echo cancellers should have a built-in safeguarding feature that controls the stability of the closed loop within the voice channel.
VOCAL Technologies Ltd developed stability control features for echo cancellation. These features can be included into software product delivery as required for the given project.