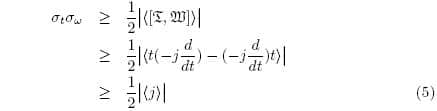Real-time Acoustic Echo Cancellation (AEC) can often be improved through the use of subband decomposition, in which the input signal is grouped into smaller segments that are processed individually. For Acoustic Echo Cancellation, such a decomposition can itself be improved by considering psychoacoustic and physiological constraints that shape human audition. One example is the gamma family of filters, specifically the gammatone and the optimal gammachirp.
Gammatone Filter
Prior to the gammachirp filter, the gammatone filter was derived to simulate the impulse response of the auditory nerve fibers [1]. Its impulse response is given by:
Where a is the amplitude, b and n are parameters that define the envelope, fc is the center frequency, ϕ is the initial phase and ERB is the equivalent rectangular bandwidth of the filter. The ERB is a psychoacoustic parameter that models the width of the auditory filter centered around the frequency fc:
The gammatone’s higher order extension, called the gammachirp filter, can improve the gammatone’s ability to represent level differences. The gammachirp filter is defined as:
Where fr is the asymptotic frequency, and the c ln(t) term is the monotonic frequency modulation term. The gammachirp filter is superior because it is the result of applying operators to derive the minimal solution to the time frequency problem.
Gammachirp Optimality
With T = t and W =-j(d/dt) as the time and frequency operators in the time domain, their commutator is defined as:
![]()
The Uncertainty Principle tells us that time and frequency cannot be measured independently:
With σ the standard deviation, and the average ‹∙›. Thus since the commutator is non-zero, there exists a floor on the time-frequency resolution. Therefore, we must be satisfied with a minimal value found by solving:
![]()
Whose solution s(t) is the gammachirp function [2].
Real Time Implementation
For any real-time acoustic echo cancellation filter bank implementation, directly applying the gammachirp is computationally burdensome. As [3] points out, a simplification can be derived by considering the fourier domain decomposition of the gammachirp:
![]()
Where FT is the Fourier transform of the gammatone filter, and HA is called the asymmetric function. Computationally efficient methods for both elements of the product exist. For instance, the gammatone filter’s frequency response can be approximated by [4]:
![]()
As f0/b is sufficiently large in the human auditory system, we can simplify the above equation as:
![]()
Thus a general nth order Gammatone filter can be created by cascading order 1 filters of the form:
![]()
Which is just a simple frequency shifted low-pass filter. Using Parseval’s relation, and the assumption that FT is symmetric, we can find the proportionality constant αN:
![]()
The asymmetric function can be described as a cascaded second-order filter [3]:

Where:
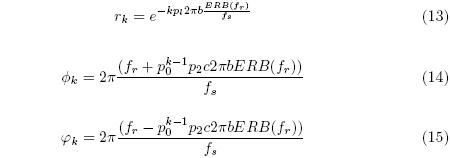
Where p0, p1, and p2 are positive constants, and fs is the sampling rate. Such a cascade is more stable than a full order method, but creates a tradeoff between stability and goodness of fit the designer of the echo canceller must consider. Thus the gammachirp filter is an optimal filterbank of time-frequency resolution, whose derivation from physiological measurements allows psychophysical simplifications for real-time implementation. Using the gammachirp filter for Acoustic Echo Cancellation results in a sub-band decomposition that is highly desirable and leads to an improved subjective experience for the listener.
References
[1] R. Meddis et al. Computational Models of the Auditory System. Spring, NY:Springer, 2010
[2] T. Irino, R. D. Patterson. “A time domain, level-dependent auditory filter: The gammachirp”, Journal of the Acoustical Society of America, vol. 101, 1997, pp.412-419
[3] T. Irino, M. Unoki. “An Analysis/Synthesis Auditory Filterbank based on an IIR Gammachirp Filter”, Computational Models of Auditory Function, 2001, pp. 317-332
[4] J. Holdsworth et al. “Implementing a gammatone filter bank”, Annex C of the SVos Final Report: The auditory filter bank, APU Report No. 2341