Signals and images compressed using compressed sensing (CS) are multiplied by a sampling matrix in order to both sample and compress the signal. To reconstruct the signal at the receiver, the original sampling matrix must be known. This paper investigates how difficult it would be for an eavesdropper to determine the content of an image with only a couple of realistic assumptions about the signaling system.
First, we assume that the eavesdropper knows the following information:
- That the signal is compressed using this CS system.
- The SIZE of the original image in pixels. This is realistic for standardized systems (i.e. fax), and may be able to be determined for other systems.
- The format of the sampling matrix (structured, binary, Gaussian, etc).
- How the sampling matrix is generated from an encryption key (if one is used).
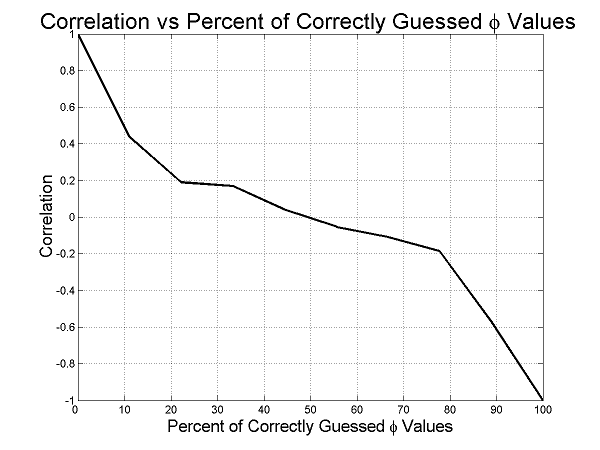
Second, we are assuming that the recovery of an image with more than a 0.2 correlation with the encrypted image constitutes breaking the encryption. This definition is required because, as can be seen in Figure 1, it is possible to decode a partial image using partial information. Figure 1 is generated using a normalized binary sampling matrix, i.e.
|
where Φ is the sampling matrix, N is the number of pixels in the image and M is the number of CS samples needed to represent the image. This format causes the symmetry about the 50% mark, which means that a guess which is 90% wrong is as useful to an attacker as one which is only 10% wrong, since it essentially results in the negative of the image being reproduced.
|
where K is the number of entries in the sampling matrix. If the sampling matrix does not need to be transmitted and can be written directly to the sender and receiver at initialization, K = M × N. For a 512 × 512 pixel image and a 25% sampling rate, K ≈ 17 × 109 with a standard deviation of 3.8 × 10-6. For this case, the probability of guessing even 51% correct is essentially 0.
If the encryption needs to be set up within a network, this solution will not work since the entire matrix will be bigger than the encrypted image. Instead, a key is used to generate Φ at the sender. This key is then transmitted to the receiver, where Φ is again generated. The security in this case is based on both the security of the key exchange protocol and the length of the key. For example, a 128 bit key has 2128 possible bit combinations. Using the equation from above, this results in a standard deviation of 0.044. Though this is not nearly as good as that obtained from the previous case, there is still less than 1.1 × 10-15 probability of guessing even 51% correct.