Fast And Efficient GCC Algorithm For Speech AOA Detection

Resolution of the angle of arrival of speech signals impinging on a microphone array is critical for beamforming and noise reduction in online applications. Due to computation and memory constraints of embedded DSPs, an efficient but fast algorithm is required to achieve any meaningful gains for beamforming. In speech processing, frame lengths on orders of $10$ milliseconds are typical, further buttressing the need for a quick resolution of algorithms. 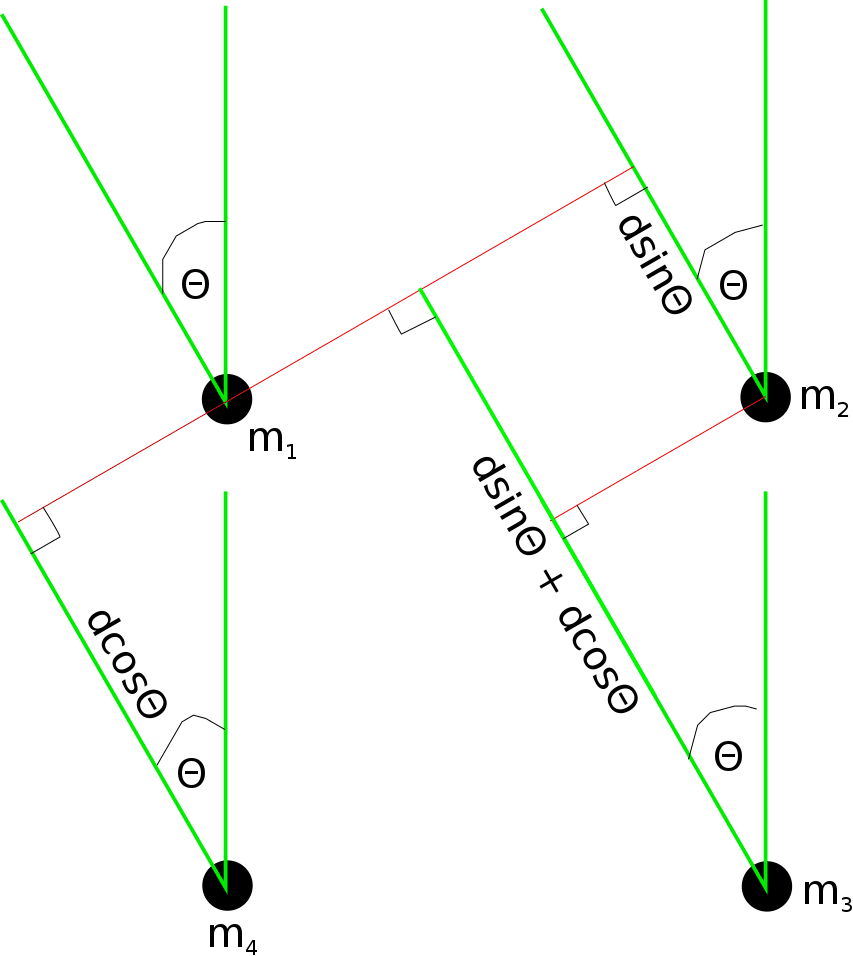The problem we wish to tackle is as follow: Given $M$ frame recordings of a single source of speech, one frame recording for each microphone, each frame having $N$ samples, determine the angle of arrival of the signal assuming a far field model. Figure 1 illustrates a typical microphone array.

Figure 1: Square microphone array.

We limit our analysis to the $2$ -D case for brevity of presentation. The general approach is to use cross-correlation to find the delay between paired microphones. GCC-PHAT however requires $\mathcal{O}(\hat{N}\log_2{\hat{N}})$ additions and multiplications because the DFT’s of both signals need to be computed. Here, $\underset{m \in \mathbb{Z}}{\mathrm{argmin}}~ \hat{N}=2^{m}\ge N$ . A faster approach will be to find the cross-correlations by leveraging the known maximum delay between a pair of microphones. This approach reduces the number of computations to $\mathcal{O}(NL)$ , where L is the maximum number of samples that can be delayed. The maximum delay on a typical DSP platform with a microphone spacing of $40mm$ will be as small as 2 samples using a sampling rate of $16kHz$ , thus making our approach at least 4 times faster than the so called GCC-PHAT and other DFT based approaches. For the illustrated microphone array in Figure 1, define the time delay between microphone $i$ and microphone $j$ as $\tau_{i,j} =t_j - t_i,\{i,j\} \in \{1,\cdots,4\}$ , with $t_i$ and $t_j$ being the arrival times of a common sample data. Define the speed of sound as c. Let $d$ be the distance between consecutive microphones $m_i$ and $m_j$ , as labeled on Figure 1, such that $|i-j| = 1$ . Also let the distance between $m_i$ and $m_j$ be $\sqrt{2} d$ for $\mod{(|i-j|,3) =2}$ . Then the time difference of arrival of signals at the microphone arrays obey the following:

$\begin{bmatrix}\tau_{1,2}, \tau_{1,3}, \tau_{1,4} ,\tau_{2,3} , \tau_{2,4} , \tau_{3,4}\end{bmatrix}^T = \frac{d}{c} \begin{bmatrix}\sin{\theta},\sin{\theta} + \cos{\theta},\cos{\theta} ,\cos{\theta} ,\cos{\theta}-\sin{\theta} ,\sin{\theta}\end{bmatrix}^T$

Here, the $\tau_{i,j}$ ‘s are estimated using pairwise correlations using:

$\underset{k \in [-L,L]}{\mathrm{argmax}}~ crr[k] = \sum\limits_{n=1}^{N} x_i[n]x_j[k+n], i \neq j, \{i,j\} \in \{1, \cdots, M\}$

where the $x_i[n]$ ‘s are sampled data $n$ at microphone $i$ . The inter-sample delays may also be dealt with by simply using the adjacent bins near the peak. For example, suppose the peak of the correlation was at the $k^{th}$ sample, then we will use the intersample value of:

$\hat{k} =\frac{2k crr[k]-(k-0.5)crr[k+1]-(k+0.5)crr[k-1]}{2crr[k]-crr[k-1]-crr[k+1]}.$

As a custom design house, VOCAL Technologies’ angle of arrival algorithms are applicable to a wide range of the microphone arrays that exist in reverberation environments. The selection of the algorithm is based on the requirements of the application and the available hardware configuration.

Complete Communications Engineering

Fast And Efficient GCC Algorithm For Speech Angle Of Arrival Detection

More Information