Differential beamforming using two microphones, and hence first order, has two different implementations. The first involves a delay of one microphone signal then taking the difference between the resultant and the second signal. An alternate to this approach is the so-called adaptive differential microphone array beamforming which forms two cardioids and combines them for the required spatial beam pattern.
Consider a two microphone array as shown in Figure 1:
Figure 1: Two microphone array
The DMA beamforming is an optimization problem to meet constraints for N microphones. For two microphones, the constrainst are used to form:
and
where is the desired beam direction and
is a desired null direction. Given
and
, the choice of
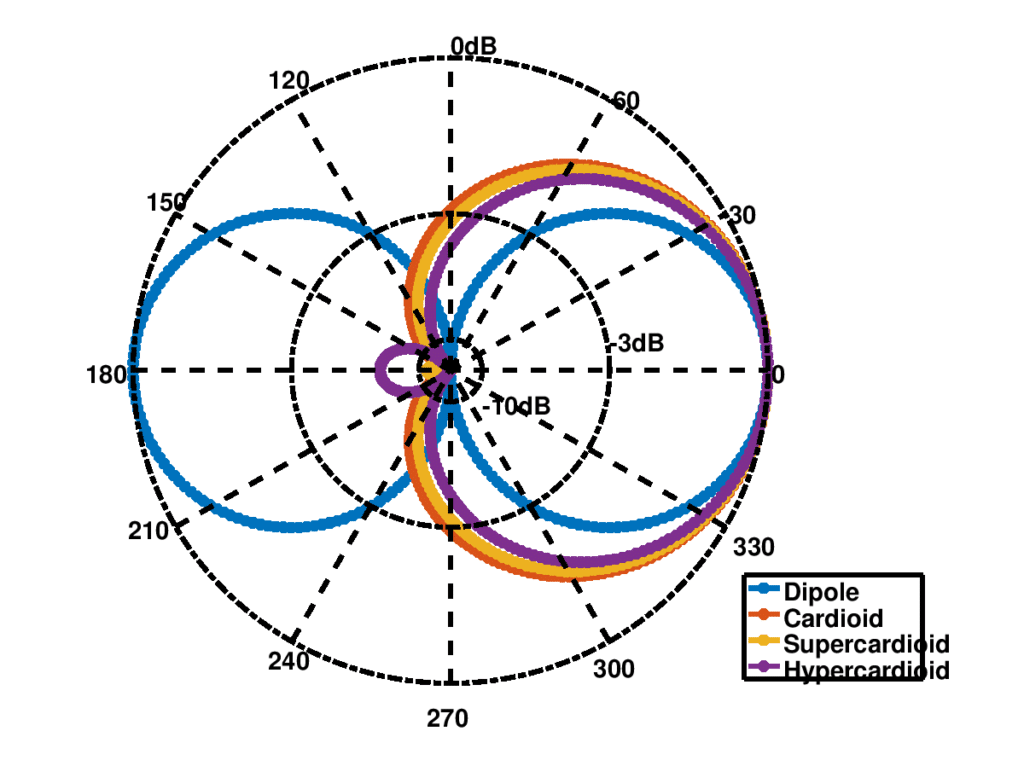
will determine whether the spatial beam will be a dipole, cardiod, hypercardiod or supercardiod. The final solution is given as
where is a design parameter to shape the beam in the direction of the source signal. The optimal value for
can be derived using a second cost function
. It can be easily shown that the optimal value of
will satisfy
Figure 2 below illustrates these 4 spatial beams.
Figure 2: Different spatial patterns
VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!