Double-talk detection based on orthogonality principle

The use of energy comparison to detect double-talk (cross-talk) can detect both the presence of a near-end speaker and a non-convergent echo. Energy detection schemes however,cannot discriminate between the two. Under the assumption that the the desired near end speech is uncorrelated with the far-end speech, the inner product of the error signal and the near end signal can be used to detect double talk.
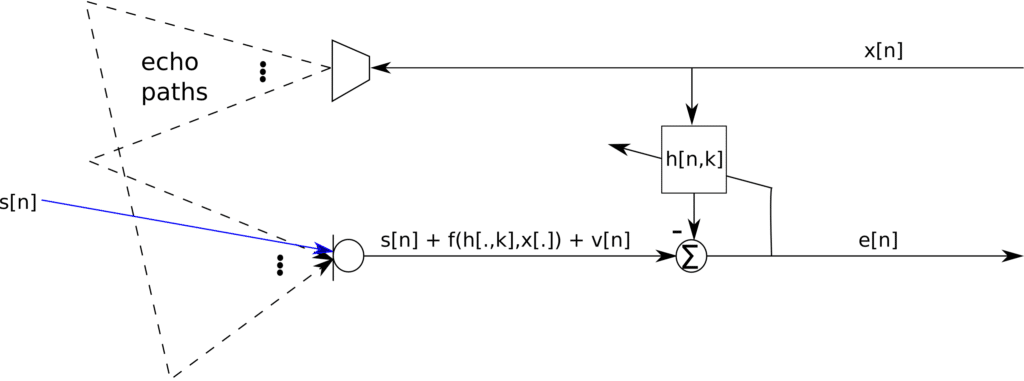
Consider the systems depicted in Figure 1 below:

Figure 1: Single line AEC architecture

$x[n]$ is the far end speech whilst $s[n]$ is the near-end speech. Denote a frame of far-end speech with accompanying echo path filter as:

$X[n]= [x[n], \cdots, x[n-L+1]] ^T$

$W= [w_0, \cdots, w_{L-1}] ^T$

Then the received near-end microphone signal is:

$y[n]= X[n] ^TW + \alpha s(n) + v(n), \alpha \in [0,1], \alpha \in \mathbb{Z}$

where $v[n]$ is zero mean i.i.d. ambient noise. The error signal is given as:

$e[n] = \alpha s(n) +X[n] ^T(W -\hat{W})+ v(n)$

where $\hat{}$ denotes the estimated variable. We are interested in the expectation of the cross product between the error signal and the microphone signal, thus:

$\mathbb{E} [e[n]^T y[n]] = (W -\hat{W})^T R_{xx} W$

It can be seen that with a convergent filter, $y[n]$ is orthogonal to the error signal. Under the assumption that he near end and far end speeches are orthogonal, The the time-frequency domain representation becomes $(W -\hat{W}) \neq 0$ when there is near end speech, hence $\mathbb{E} [e[n]^T y[n]] \neq 0$ . The orthogonality based detection scheme is then given as:

$\beta[n] = \begin{cases} 1, & \mathbb{E} [e[n]^T y[n]] \ge \gamma \\ 0, &otherwise \\ \end{cases}$

where $\gamma > 0$ is a threshold parameter. A window is most times applied to remove spurious noise in the detection scheme.

VOCAL Technologies offers custom designed solutions for AEC with a robust double-talk detection, voice activity detector, beamforming and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific task. Contact us today to discuss your solution!

Complete Communications Engineering

Double-talk detection based on orthogonality principle

More Information