Brief Introduction to Ambisonics

Ambisonics is a spatial audio technique used to record, reproduce, or simulate a sound field. This method takes advantage of the well-known Kirchhoff-Helmholtz integral equation (KHIE). Knowing the pressure and normal particle velocity at a point on an enclosed volume surface, KHIE allows us to evaluate the sound pressure at any position inside or outside the boundary. Ambisonics uses the simplest geometric volume, a sphere.

From the Ambisonic recording, the measured soundfield is decomposed at a given point using an $L^{th}$ -order spherical Bessel series, yielding

$p(k,r,\theta,\phi) = \sum_{n=0}^L\sum_{m=-n}^n\text{i}^nj_n(kr)A_{nm}Y_n^m(\theta,\phi)$

where n is the degree, m is the order, $A_{nm}$ is the Ambisonic coefficient, and $j_n\left(kr\right)$ is the Bessel function of the first kind representing the radial-dependence of the signal. Angular-dependence (azimuth and elevation) is represented by spherical harmonics,

$Y_n^m(\theta,\phi) = \sqrt{\frac{2n+1)}{4\pi}\frac{(n-m)!}{(n+m)!}}$

where $P_n^m(\cdot)$ are the associated Legendre functions, and the radical is the normalization factor. The expansion is also truncated to an order L , giving $N\geq\left(L+1\right)^2$ , where N is the number of sensors or loudspeakers used to measure or project the soundfield, respectively.

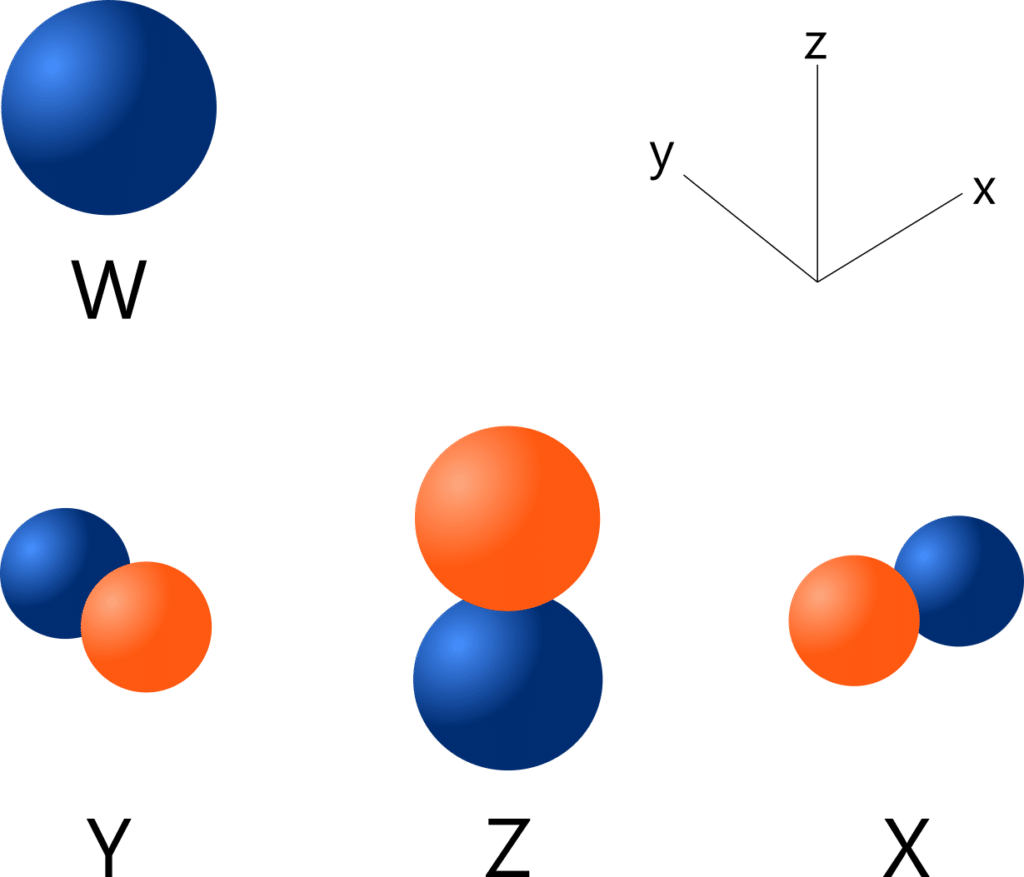
Figure 1. First-order Ambisonics.
W is order n=0, degree 0, Y is n=1,
m=-1, Z is n=1, m=0, and X is n=1,
m=1.

Solving for the Ambisonic coefficients allows us to encode the signal from A-Format (raw signals) to B-Format. Traditionally, B-Format is restricted to first-order Ambisonics, as seen above; however, many other formats have extended to higher orders, such as FuMa and AmbiX. Lastly, Ambisonics most prominent feature allows for agnostic playback. Loudspeaker configurations may use any arbitrary geometry; the configuration is only limited by the quantity of speakers. Ambisonic signals may also be rendered binaurally through headphones.

Complete Communications Engineering

Brief Introduction to Ambisonics