Ringing is a visual artifact that appears during image upscaling in flat or smooth areas near strong edges. The greater the upscaling ratio, the more visible the artifact. It looks like a ghost of the strong edge on the flat or smooth area.
One common approach to scaler implementation uses polyphase filters. For simplicity, consider one dimensional scaling (vertical or horizontal). Assume the distance between input pixels is one. The output upscaled pixels are located with greater density than the input pixels (assuming the input and output images have the same physical size), so output pixels will be located between input pixels.
The output pixel value is a convolution of the set of N input pixels located before and after (N/2 before and N/2 after, where N is an even value) and the FIR filter is a phase m filter of the polyphase filter. The phase m is defined by the location of the output pixel with respect to the two closest input pixels.
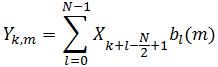In this formula, Xk is the input pixel value with coordinate k, Yk,m is the output pixel value corresponding to phase m and located between input pixels with coordinates k and k+1, and bl(m) are the polyphase filter coefficients for phase m.
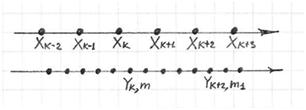
For example, if N=6 the output pixel Yk,m is specified by the following input pixels:
Xk-2, Xk-1, Xk,Xk+1, Xk+2, Xk+3.
If pixels Xk-2, Xk-1, Xk, and Xk+1 correspond to a flat or smooth area and Xk+2 and Xk+3 correspond to a strong edge, the output pixel will show ringing.
To solve this issue, a deringing technique can be applied. The technique will analyze differences between adjacent input pixels and modify the input pixel values to reduce the influence of strong edges.
If |Xk-2 – Xk-1|, |Xk-1 – Xk| and |Xk – Xk+1| have small values and |Xk – Xk+3| has a big value, the value Xk+3 is modified to reduce |Xk – Xk+3|.
If |Xk-2 – Xk-1|, |Xk-1 – Xk| and |Xk – Xk+1| have small values and |Xk – Xk+2| has a big value, the value Xk+2 is modified to reduce |Xk – Xk+2|.
If |Xk+3 – Xk+2|, |Xk+2 – Xk+1| and |Xk+1 – Xk| have small values and |Xk – Xk-1| has a big value, the value Xk-1 is modified to reduce |Xk – Xk-1|.
If |Xk+3 – Xk+2|, |Xk+2 – Xk+1| and |Xk+1 – Xk| have small values and |Xk – Xk-2| has a big value, the value Xk-2 is modified to reduce |Xk – Xk-2|.