Non-aliased TDOA angle of arrival estimation

Most beamforming techniques are reliant on signal manipulation from a uniform linear array of microphones. $N\ge 3$ collinear microphones can only estimate angle of arrivals $\theta \in [0, \pi)$ and cannot deal with the other half plane of $\theta \in [\pi, 2\pi)$ . The lower half plane is aliased to the upper half plane. Three non-collinear microphone array is sufficient to deal with this problem in $2-$ D.

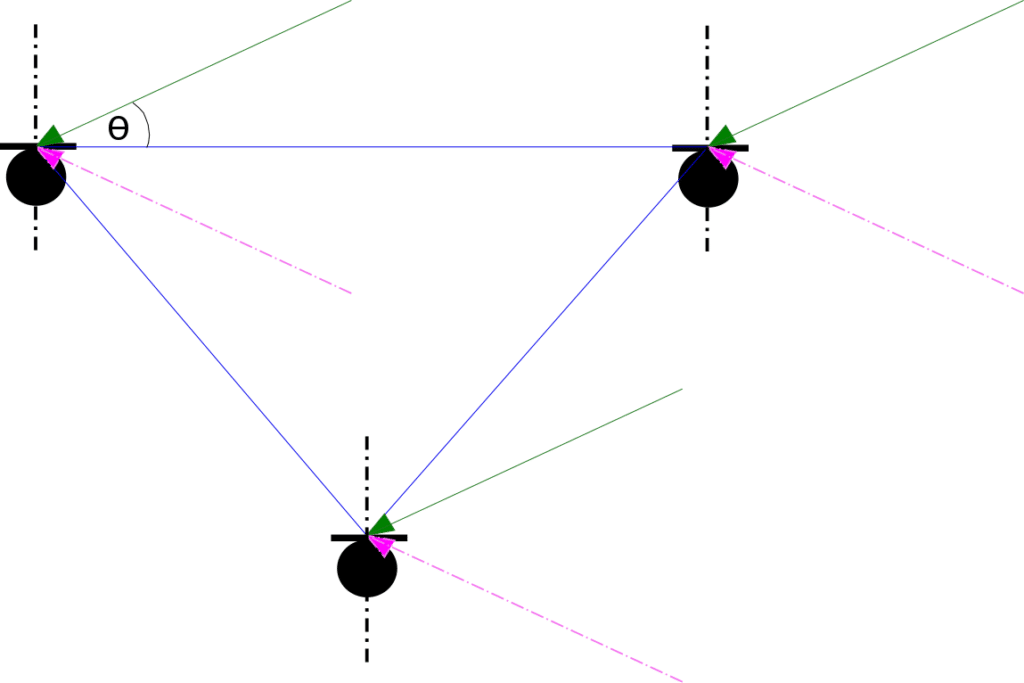
Consider a far field acoustic signal impinging $3$ non-collinear microphones with pairwise separation distance $d$ at an angle of $\theta^{\circ}$ . The signal at microphone $i$ , $x_i$ , can be denoted as

$x_i(t) = h_i \ast s(t - \tau_i) + \nu_i(t), i \in \{1, \cdots, 3\}$

where $h_i$ is the channel impulse response, $\ast$ denotes convolution, $\tau_i$ is the delay at microphone $i$ , $s(t)$ is the source signal and $\nu_i(t)$ is a zero mean ergodic process. The setup is as shown in Figure 1.

$3$ non-collinear microphones with pairwise distance of $d$

Define the time delay between microphone $i$ and microphone $j$ as $\tau_{i,j} =t_j - t_i,\{i,j\} \in \{1,\cdots,3\}$ , with $t_i$ and $t_j$ being the arrival times of a common sample data. Define the speed of sound as $c$ . Given this setup, there are two possibilities: either the signal is from the upper half plane, or, the signal is from the lower half plane. Suppose the signal is from the upper half plane, then the time difference of arrival of signals at the microphones obey the following:

$\begin{bmatrix}\tau_{1,2} \\ \tau_{1,3} \\ \tau_{2,3} \end{bmatrix} = \frac{d}{c} \begin{bmatrix}\cos{\theta} \\ \cos{(\frac{2}{3} \pi -\theta)}\\ \cos{(\theta-\frac{1}{3} \pi)} \end{bmatrix}$

If however, the signal was from the lower half plane, then the microphones obey:

$\begin{bmatrix}\tau_{1,2} \\ \tau_{1,3} \\ \tau_{2,3} \end{bmatrix} = \frac{d}{c} \begin{bmatrix}\cos{\theta} \\ \cos{(\frac{1}{3} \pi -\theta)}\\ \cos{(\frac{2}{3} \pi - \theta)} \end{bmatrix}$

The $\tau_{i,j}$ ‘s will be estimated using pairwise correlations. We use either of the two equations above based on the signs and relative magnitudes of $\{\tau_{1,3},\tau_{2,3}\}$ .

VOCAL Technologies offers custom designed AoA estimation solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

Complete Communications Engineering

Non-aliased TDOA angle of arrival estimation

More Information