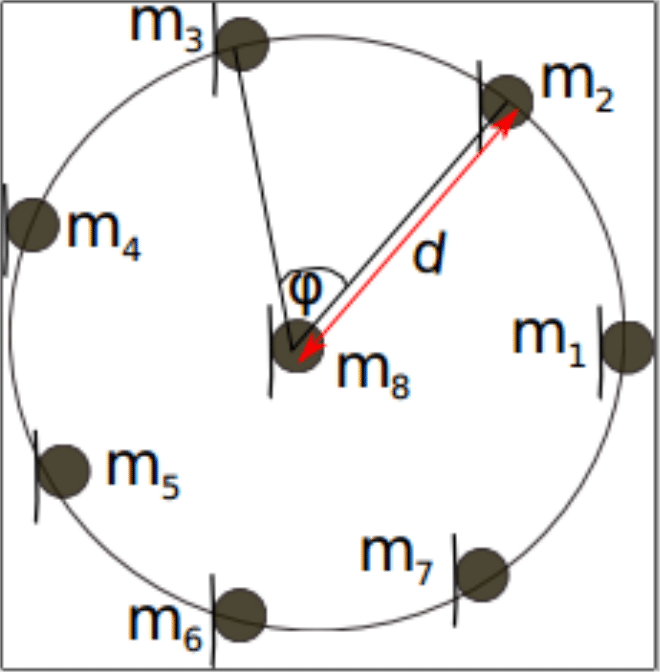
Fast Beamformer With Fixed Direction For Circular Array Mics

We show an approach to beamforming an acoustic source using a circular microphone topology. Consider the circular array illustrated in Figure 1 below and suppose a beamforming solution is desired.

Figure 1: Circular microphone array topology for $8$ microphones, $\psi= \frac{2\pi}{7}$ .

Define the angle of arrival to be the impinging angle at microphone $m_{8}$ as $\theta$ , using the line joining microphones $m_1$ and $m_8$ as reference. By choosing every consecutive pair of microphones together with the center microphone, 7 triples are possible. Each triple can be said to have an effective look direction width of $\frac{2\pi}{7}$ . Thus anytime the signal of interest falls withing this range of any triplet, we chose these triplet to form the beam. Then by averaging the received signals at three microphones, it can be easily shown to that;

$Y(w) = \frac{1}{3} \sum\limits_{q} X_{q} (w) = X_0 (w) H(w) + \frac{1}{3}\sum\limits_{q} N_q(w)$

where

$X_{q} (w) = X_0 e^{-jw\tau_{8,q}} + N_{q} (w)$

Here, $\tau_{8,q}$ is the delay between microphones $8$ and $q$ , $H(w)$ is the effective “sum filter”.

$H(w)$ can be synthesized as:

$H(w) = \frac{2}{3}\cos{\left( w \frac{d}{c} \sin{\frac{\psi}{2}} \sin{\theta} \right)}+ \frac{1}{3} e^{-jw \frac{d}{c} \cos{\frac{\psi}{2}}\cos{\theta}}$

Suppose we sum the signals at the three microphones, then we can use the above filter to form a distortionless response for the desired signal. An approximate inverse filter can be used with minimal distortion across all frequencies. Define such a filter as

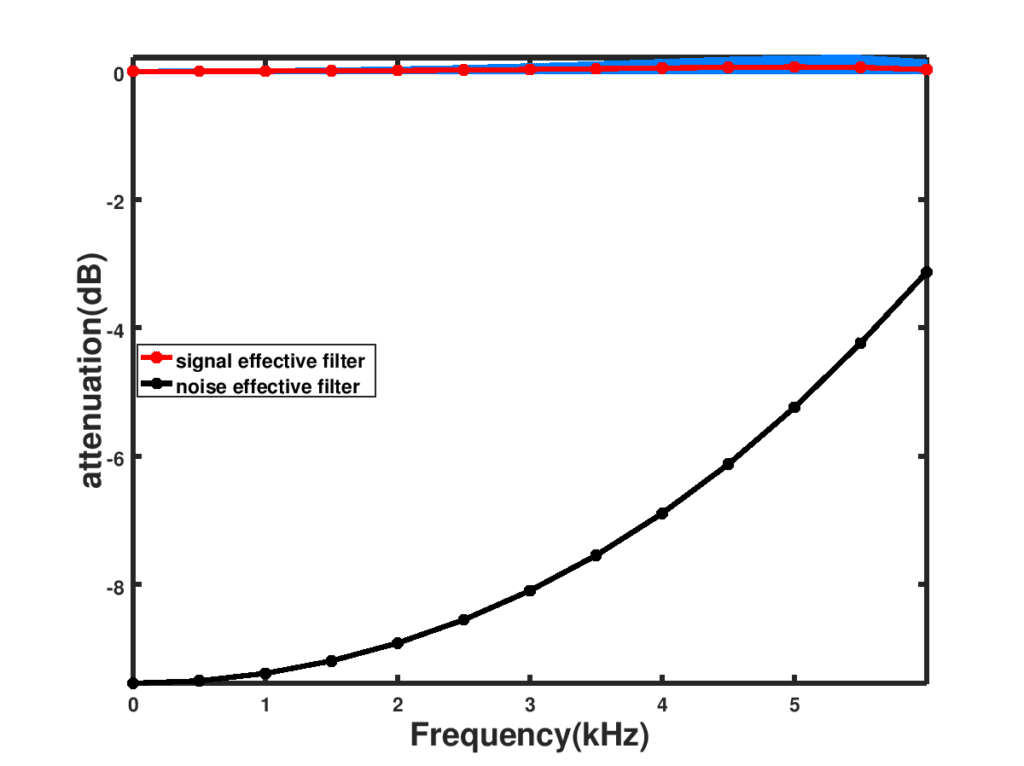
$H^{-1}(w) = \frac{3}{ 2\cos{\left( w \frac{d}{c} \sin{\frac{\psi}{2}} \sin{\theta} \right)}+ e^{jw \frac{d}{c} \cos{\frac{\psi}{2}}\cos{\theta}} }$

The effective magnitude response of the above approach, for each triplet, is as shown in Figure 2 below:

Figure 2: Effective magnitude response for desired signal and noise.

VOCAL Technologies offers custom designed solutions for beamforming with a direction of arrival estimation, robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

Complete Communications Engineering

Fast beamformer with fixed direction for circular array microphones

More Information